数式処理ソフト　DERIVE（デライブ） de ドライブ

８７．道中双六の問題（補筆3）（今後の課題）

目次

　はじめに
　道中双六の問題の概要
　　　ルールなど
　　　宿場数が1の場合（c=2)
　　　宿場数が2の場合（c=3)
　　　宿場数が3の場合（c=4)
　　　宿場数が一般の場合（c=宿場数＋1）
　課題0　一般の場合の式表示の近似式を求める
　偏微分方程式としての扱い
　　　課題1　p=1/2の場合の解と差分解との比較
　　　課題2　p<>1/2の場合の方程式の整理と見合う境界条件
　課題3　対称型道中双六の問題
　　　宿場数が1つずつの場合・2つずつの場合
　課題4　フィードバック回路
　課題5　マルコフ過程等

はじめに

「またまた、更新が遅くなってしもうたな。
　去年の春以降、プライベートでいろいろとあったものじゃからな」

「ホント、DERIVE de ドライブの更新は、約1年ぶりになってしまったわね。
　前回は、2017年の4月だから。
　それが、第86回の「偏微分方程式の解法（1）（関数変換、変数変換、積分変換）」、これね」

「ともちゃんかい。
　ここんところ、『今月のご挨拶』以外では、ご無沙汰してしまったのう。
　後で少し触れるが、第85回及び86回の記事に基づいて、道中双六の問題の計算を進めてみたのじゃ。
　すなわち、宿場毎に進む確率 p が1/2 と等しくない場合じゃが、方程式自身の変形は、問題ない。
　しかし、境界条件について、あらためて、検討すると、どうも、第85回までで考えていたのは、少し違うのではないかとも思われた。
　そこで、もう少し、視野を広げて、今後、検討したいテーマを列挙してみようと思ったのじゃ」

「たとえば、どんなこと？」

「そうじゃな。
　ともちゃんは、『ランダムウォーク（酔歩）』というのは、聞いたことがあろう。
　花粉を水に浸したときに、そこから水中にしみ出してくるデンプンの微粒子（粒径=数ミクロン）が小刻みに震える現象が『ブラウン運動』じゃ。
　1872年にイギリスの植物学者『ロバート・ブラウン』が発見したが、その震える原因が不明じゃった。
　その後、振動は、水分子のランダムな衝突により引き起こされておるということが分かった」

「ブラウン運動のデンプン粒子については、第72回の『常微分方程式の数値解法（初期値問題）（1）』の『ルンゲ氏、クッタ氏と四方山話』で触れているわね。
　当該個所の抜粋を下注に示すわ」

「このような運動を数学的に定式化したものが、『ランダムウォーク』じゃ。
　ランダム・ウォークは、日本語では、『酔歩』とも訳されているが、あたかも、酔っ払いがふらふらと歩いている様のようにもたとえられるからじゃな。
　ブラウン運動をマクロな視点でとらえると、拡散方程式の一例とも考えられる。
　さらに、これらは、マルコフ過程、あるいは、拡散過程と言われる大きな分野に属する話なのじゃ」

　目次へ戻る

注　ブラウン運動
　ブラウン運動」（水中の微粒子が水分子の衝突により細かく揺れ動く運動）は、1827年に、植物学者 R.Brown氏が花粉から出てくる「微粒子」が細かく揺れ動く様を観察したことにより、その名称が付いた。後年、それが「分子」の存在を証拠立てたことで有名になった。
　水中に入れた花粉（粒径：30～50ミクロン）から出てくる微粒子（数ミクロン程度）が水分子の衝突により揺れ動くのであって、花粉そのものは、大きくて重いので動かない。ブラウンの原論文には、花粉と微粒子とは、はっきりと区別されて記述されているそうじゃ。
　最近の書籍では、「水中に浮かぶ花粉から出てくる小さな粒子が・・」と書かれているものもある。（物理学大事典：鈴木增雄・荒船次郎・和達三樹 編：朝倉書店：2006年2月第2刷）。
　この花粉から漏れ出す微粒子は、デンプンなどの大きな分子じゃそうだ。デンプンとは、炭水化物に属し、分子式は、（C6H10O6）nという多糖類である。　

道中双六の問題の概要

ルールなど

「では、わたし、ともちゃんが解説しますね。
　そもそも、道中双六の問題は、おじぃさんの2014年の年賀状のテーマだったのね。

　この年は、午年。そこで、いきなり、脱線してしまうけど、
　干支は、日本では、子・丑・寅・卯・辰・巳・午・羊・申・酉・戌・亥 でしょ。
　他の国では、少しメンバーが違っているんだって。
　たとえば、中国では、亥・猪は、豚を意味する漢字なんだ。
　豚は、イノシシを家畜化した動物で、中国では、豚は、食用として一般的なので、猪は、豚を表した。
　しかし、日本では、昔、豚がいなくて肉食の習慣もないので、野生のイノシシの方が身近だったためらしい。
　他に、ベトナムでは、牛は、水牛だし、ロシアでは、兎が猫なんだそうよ。
　※『中国語スクリプト』の中国の干支と十二支：http://chugokugo-script.net/kiso/eto.html）より」

「ともちゃんや。
　この双六は、振り出しから、いっこうに進まないのう」

「ご隠居様。
　もう少し、お待ちくださいな。
　さてと、下のような絵双六で駒を振り出しから進めることを考えます。



　ここで、図のように、上がりまでに宿場が1 個以上ある場合を考えるとき、
　１．駒は、振り出しから、確率1で、1番目の宿場に進むことができる。
　２．駒は、各宿場で、確率 pで、次の宿場に進み、確率 (1－p)で1つ戻るものとする。
　３．駒が最後の宿場から上がりに進んだときは、双六上から消える。（上がりから戻ることはない）
　４．駒どおしの関係は、無いものとする。
　５．振り出しから宿場まで、各宿場間、最後の宿場と上がりまでの所要時間は、同一とし、1（日）と勘定する。
　というルールで双六を行うと、平均日数は、最短日数の何倍かを計算したかったという訳」
　目次へ戻る

宿場数が1の場合（c=2)

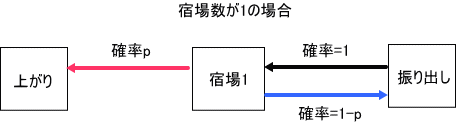
「上がりまでの日数をm、その確率をf（m）で表すと、m=0～の整数として、
　最速日数である 2の確率 f（2）=p、はすぐに分かる。
　f（3）はゼロで、f（4）=p（1－p）、以下同様に、f（2m+2）=p（1－p）^m、である。
　従って、平均日数は、Σ（m=0～∞）（m×f（m））=Σ（2m+2）p（1－p）^m=2/p となる。
　なお、ここで、進むのと戻るのが同確率 p=1/2の場合は、平均日数は、4（日）となるのね」

「つまり、最短日数2日の2倍じゃな」
　目次へ戻る

宿場数が2の場合（c=3)

　「次に宿場数が2の場合ね。


　
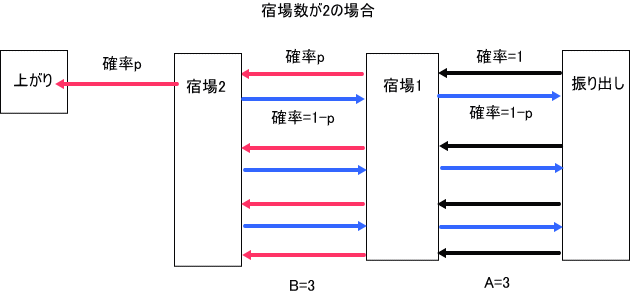
　この場合は、『道中双六の問題（続々）』の『（1）宿場数が1及び2のケースのおさらい』で、丁寧に扱っているので、再掲すると、
　振り出しから上がりまでの日数は、2m+3 日（m=0、1、・・）であることは、すぐに分かる。
　振り出しと宿場1の間の折り返しの組数をA、宿場1と宿場2の間の折り返しの組数をBとしたとき、各折り返しでは、1回の折り返しについて、2日を要する。
　そのため、　2m+3＝2A＋2B＋3、である。
　ここで、右辺で、3を加えているのは、区間1（振り出し＋宿場1）、区間2（宿場1から2まで）及び最後の区間（宿場2から上がり）において、それぞれ1日を別に必要とするからですね。
　従って、A＋B＝m、が成り立つ。
　上の図では、A=3、B=3、の場合の例を示している。
　2m+3日で上がる確率、f（2m+3）=Σ（A+B=m）（1－p）^A×（1－p）^B×p^（B＋1）×p、
　ここで、
　赤字の（1－p）^A は、宿場1から振り出しに戻される確率、
　青字の（1－p）^B は、宿場2から宿場1に戻される確率、
　緑字のp＾（B＋1） は、上がるために宿場1から2に進む確率、
　最後のp は、宿場2から上がりに進む確率、
　となっているのね。

　注意するべきなのは、振り出しから宿場1へは、確率1ですすめること。
　これより、f（2m+3）=Σ（A=0～m）Comb（m，A）（1－p）^m p^（m－A＋2）、
　※ Comb（m，A）は、組み合わせの数を表すDERIVEの関数。
　f（2m+3）=（1－p）^m p^2Σ（A=0～m） Comb（m，A）p^（m－A）×1 、と書き直せば、
　赤字部分が（1＋p）^m と等しいことが分かる。
　よって、f（2m+3）=p^2×（1－p）^m×（1＋p）^m=p^2×（1－p^2）^m、とまとめられる。
　これにより、平均日数は、
　Σ（m=0～∞）（2m＋3）×p^2×（1－p^2）^m=1＋2/p^2、と計算できたのね。
　なお、p=1/2の場合は、平均日数が 9（日）となる。
　すなわち、最短日数3日の3倍ね。

　今まで、特に注意してこなかったけど、重要な注意点があるわ。
　双六の全体の長さが一定の場合は、宿場数が増えると、その1日の絶対的な長さは、小さくなること。
　なぜかって言うと、最初に挙げたルールの6番で、宿場間の移動に要する時間を1日と定義しているためね。
　これは、駒の進む速さが低下するとも言えるわ。
　一方、1日の長さは一定と考えた場合は、宿場数が増えると、双六の全体の長さは、大きくなる。
　そのため、問題では、平均日数が最短日数の何倍か、を問うことで、規格化しているんだけどね。
　ま、本当は、ルールを追加して、このどちらかなのかを明らかにした方がよかったかも知れないわ」
　目次へ戻る

宿場数が3の場合（c=4)

「宿場数が3の場合は、mを0以上の整数として、2m＋4日目に上がる確率は、下の式になる。
　※『道中双六の問題（続々）』
　f（2m+4）=（1－p）^m p^3 Σ（A+B+C=m）（p^（m－A）Comb（A+B，A） Comb（B+C，B））、
　ここで、A、B、Cは、0以上の整数、Comb関数は、組み合わせ数を計算するDERIVEの関数。
　下図で、この計算式を説明しますね。

　
　
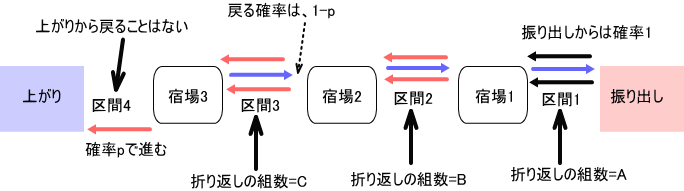
　区間1から3までの、折り返しの組数を図のように、A、B、C としている。
　この3つの数がある一つの組（合計がm）の場合、上がる確率への寄与は、
　区間1では、（1－p）^A 、
　区間2では、（1－p）^B ×p^（B+1）、
　区間3では、（1－p）^C ×p^（C+1）、
　区間4では、p、
　となるため、
　区間1から4まででかけ算して、
　（1－p）^（A+B+C） ×p^（B+C）×p^3、となり、ここで、A+B+C=mを使えば、
　（1－p）^m ×p^（m－A）×p^3、となるの。
　これを足しあわせれば良いのだけど、A+B+C=m、という条件だけでは、1つのm に対して、様々な異なったパターンがあるところが面倒。
　宿場数が2の場合は、mからAをとる組み合わせの数、Comb（m，A）、だけで良かったんだけどね。
　一見、この係数は、Comb（m，A）×Comb（m－A，B）、で良いように思える。
　この係数は、いわゆる多項係数、すなわち、m！/（A！B！C！）、と等しいんだけど。
　大切なのは、戻る場合があることね。
　戻る場合は、一つ手前の宿場（または振り出し）に戻るのよ。いっぺんに2つ戻ることは、ない。
　ということで、隣り合う区間同士の関係があるの。
　そのため、係数の第1項は、mをA+B、に変えて、Comb（A+B，A）とすべきなのね。
　同じように、第2項も、m－A をB+Cとして、Comb（B+C，B） とする。
　※宿場数が3の今回のケースでは、第2項は、結果的には、同じとなるんだけども。
　ただし、残念ながら、宿場数が2の場合のように、これ以上、まとめられないのよね。
　f（2m+4）=（1－p）^m p^3 Σ（A+B+C=m）（p^（m－A）Comb（A+B，A） Comb（B+C，B））、とここまで。
　よって、平均日数=Σ（m=0～n）（2m＋4）f（2m+4）、これから先は、数値計算が必要。
　たとえば、p=1/2 の場合は、平均日数は、16（日）、と計算できるので、最短日数4日の4倍というわけ」
　目次へ戻る

宿場数が一般の場合（c=宿場数＋1）

「宿場数が一般の場合は、実質的には、宿場数が3の場合にすでに書いてしまっているんだけど、次のようになる。
　※『道中双六の問題（補筆1）』では、予想式として載せている。
　宿場数＋1≡c、と置いて、mを0以上の整数として、2m＋c日目に上がる確率は、
　f（2m+c）=（1－p）^m p^(c－1) Σ（k1+k2+・・＋kc-1=m）（p^（m－k1）Comb（k1+k2，k1） Comb（k2+k3，k2）・・Comb（kc-2+kc-1，kc-2））、
　ここで、k1、k2、k3等 は、0以上の整数、Comb関数は、組み合わせ数を計算するDERIVEの関数。
　予想の段階では、c=6の場合で、後述する差分方程式を使って、上がる確率を厳密に計算して、両者が、一致することを確かめているわね。
　このf（2m＋6）のm=0～9の場合の式を見ると、
　f（2m＋6）=p^5×（1－p）^m×（pのm次式）、の形をしていて、第3項は、有理数の範囲では、因数分解ができないようだわ。
　さらに、p=1/2で、平均日数を、m=0～100まで計算し、36に近い値（35.76778393）を得ている。
　これらから、p=1/2の場合、平均日数は、最短日数（c）のc倍、すなわち、平均日数は、cの2乗と予想した訳ね」

「ともちゃん、ご苦労様じゃった。
　元の問題の解としては、書いてくれた上掲の確率の式で得られたと言っても良いじゃろう。
　平均日数＝Σ（m=0～∞）（2m+c）×f（2m+c）、と計算できるからな。
　ただし、cが今回のように、五十三次（c=54）、のような場合、pが小なると数値計算は、大変であるのもたしかじゃ。
　もう少し、解析的に計算可能な表現が望ましいので、2項分布関数が正規分布関数で近似できるように、f（2m＋c）を近似できる関数を見いだせるとよい。
　『道中双六の問題（続）』では、差分方程式も立てているんじゃが、その補助として、下図をつかったんじゃった。
　それを下図に示そう。（『道中双六の問題（補筆1）』から引用）
　
　
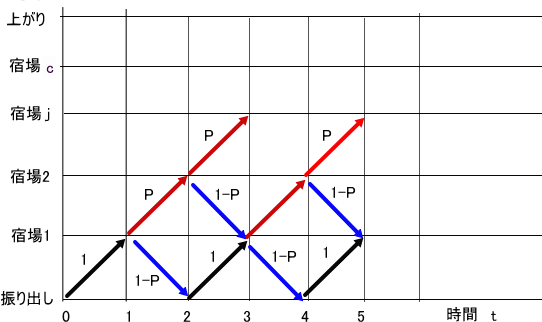
　時間をtで、振り出しから上がりまでをj（0～c）で表す。
　ただし、各宿場に至る確率をf(j,t)とし、上がり c=宿場数＋1、
　振り出し、上がりを含めて、各宿場に至る確率を、f（j，t）で表す。
　（1）f(0,0)=1
　（2）t<j → f(j,t)=0
　（3）j>c → f(j,t)=0
　（3）f(0,t)=(1－p)×f(1,t－1)
　（4）f(1,t)=f(0,t－1)
　（5）j<c－1 → f(j,t)=(1－p)×f(j+1,t－1)+p×f(j－1,t－1)
　（6）上記以外は、f(j,t)=p×f(j－1,t－1)、
　従来の表現では、たとえば、宿場数が3の場合（c=4）、
　t=2m＋4 で、上がる確率は、f（c，2m＋4）、と書くことに注意して欲しい。
　だいぶん、長くなったが、ここまでが、概要となる。
　以降は、今後の課題を述べてみよう」
※　緑字の部分は、2018/1/21　追記
　目次へ戻る

課題0　一般の場合の式表示の近似式を求める

「前節で述べたように、確率密度関数を何らかの近似関数で構成することじゃ。
　f（2m+c）=（1－p）^m p^(c－1) Σ（k1+k2+・・＋kc-1=m）（p^（m－k1）Comb（k1+k2，k1） Comb（k2+k3，k2）・・Comb（kc-2+kc-1，kc-2））、
　ここで、k1、k2、k3等 は、0以上の整数、Comb関数は、組み合わせ数を計算するDERIVEの関数。
　具体的には、右辺のΣを取り払って、p、c、m の関数として、表示する（近似）式を得ることだ」
　※　緑字の部分は、2018/1/21　追記
　目次へ戻る

偏微分方程式としての扱い

「前節の差分方程式を連続近似すると、偏微分方程式が得られる。『道中双六の問題（続々）』
　なお、2次の微少量のどの項を省略するか等は、『道中双六の問題（補筆2）』で再検証した。
　さて、方程式は、q=2p－1、とおけば、
　∂(f(x, t), x, 2)/2 ＋q∂(∂(f(x, t), t), x)－q∂(f(x, t), x) －∂(f(x,，t)，t)=0、
　ただし、ここで、c=宿場数＋1、すなわち、最短日数じゃ。
　なお、p=1/2の場合は、q=0なので、
　∂(f(x, t), x, 2)/2 －∂(f(x,，t)，t)=0、と簡単になる」
　目次へ戻る

課題1　p=1/2の場合の解と差分解との比較

「p=1/2の場合は、適切な初期条件と境界条件の下に、f を決定し、それを基にして、平均日数をc^2 と計算することができた。
　具体的には、『道中双六の問題（続々）』を参照のこと。
　また、そのページでは、残したある無限和に関する厳密な計算については、『道中双六の問題（補筆1）』で実行し検証した。
　しかし、これまで、平均日数に着目してきたため、微分方程式近似で、元の差分方程式の解（差分解）をどのぐらい近似してるのかは、比較してこなかった。
　ここは、一つ、今後の課題としたいのう」

「たしかにね。
　偏微分方程式の解は、p=1/2の場合、
　f（x，t）=Σ（k=1～∞）（2/c×cos（λk√2 x）×exp（－λk^2 t））、
　λk=（k－1/2）π/（√2 c）、と無限級数で表現されているんだけど、実際は、適当な項数で打ち切る。
　一方、差分方程式による数値計算では、Excel も活躍したわね。⇒　『道中双六の問題（続々）』、
　でも、おじぃさんが言うように、偏微分方程式の解と差分解との比較は、やっていなかった」

「では、今後の課題1、としておこう」　
　目次へ戻る

課題2　p<>1/2の場合の方程式の整理と見合う境界条件

以下、少し長いので、お急ぎの方は、次節へお進みください。

「ともちゃん、
　∂(f(x, t), x, 2)/2 ＋q∂(∂(f(x, t), t), x)－q∂(f(x, t), x) －∂(f(x,，t)，t)=0、－－－式（1）
　p<>1/2の場合に、この方程式を簡単化して欲しい」

「わかりやした。
　ま、式（1）は、第86回『偏微分方程式（関数変換、変数変換、積分変換）』で、例題として取り上げているからね。
　以下では、∂(f(x, t), x, 2) などを f xx などと、略記します。
　式（1）は、(1/2)fxx＋q fxt－q fx－f t=0、と短く書けるのね。
　ただし、ここで、q=2p－1、のパラメーター。
　第86回のDERIVEの関数流に書けば、係数ベクトルは、
　［1/2，q，0，－q，－1，0］、となるわ。
　これは、一般の2階の線形偏微分方程式を、
　A f xx＋B f xt＋C f tt＋D f x＋E f t＋F f =0、と書いたとき、その係数を、
　ベクトル ［A，B，C，D，E，F］ と表したもの。
　現在の変数［x，t］を変数変換により、新変数［u，v］に変換するんだけど、
　u=αx＋βt、v=γt、と置いて、
　第86回で作った、DERIVE のユーザ定義関数 FPDE1 を使うと、
　FPDE1([1/2,q,0,-q,-1,0],[x,t],[],[α*x+β*t,γ*t])、を計算することにより、
　[q·α·β + α^2/2, q·α·γ, 0, － q·α － β, －γ, 0]、が得られる。
　この新係数ベクトルの f xx の項をゼロとする条件は、
　q·α·β + α^2/2=0、より、
　β=－α/（2q）、が得られる。
　これにより、係数ベクトルは、
　[0, q·α·γ, 0, α/(2·q) － q·α, －γ, 0]、となったわ」

「そうじゃな。
　変数変換により、2階の項は、f xt の項のみとなった。
　α、γには、任意性が残っているので、
　α=2q、γ=1、とすれば、
　β=－1、となり、
　変数変換は、u=2qx－t、v=t、と置いたことになる。
　こうすることにより、係数ベクトルは、
　[0, 2·q^2, 0, 1 － 2·q^2, －1, 0]となった。
　一方、1階の f u、f v の項が邪魔なので、
　f=φ(u，v)×g(u，v)、ただし、φ=Exp(λu＋μv）、として関数変換を行うことにより、
　1階の項の一部を消去しよう。
　そのためには、第86回で作った関数、FPDE2を使う。
　FPDE2([0, 2·q^2, 0, 1 - 2·q^2, -1, 0], [u, v], EXP(λ·u + μ·v))
　結果、ゼロでない共通因子 Exp(λu＋μv）で除した係数ベクトルは、
　[0, 2·q^2, 0, q^2·(2·μ － 2) + 1, 2·q^2·λ － 1, 2·q^2·λ·(μ － 1) + λ － μ]、
　ここで、1階の項の係数をゼロとする条件は、
　q^2·(2·μ － 2) + 1=0、
　2·q^2·λ － 1=0、
　となるので、
　λ = 1/(2·q^2)、
　μ = (2·q^2 － 1)/(2·q^2)、とλ、μが決定できる。
　こうすると、g(u，v)に関する係数ベクトルは、
　[0, 2·q^2, 0, 0, 0, (1 － 2·q^2)/(2·q^2)]、となる。
　これは、
　∂（∂（g，u），v）=－（1－2q^2）/（4q^4）×g、－－－式（2）
　ただし、f(u，v)=g(u，v)×Exp(u/(2·q^2)＋v(2·q^2 － 1)/(2·q^2)）、を意味する。
　ここで、u=2qx－t、v=t、であるがの」

「式（2）の右辺の正負により、解が変わってくるわね。
　その境目は、右辺がちょうどゼロとな、q^2=1/2、
　すなわち、p = 1/2 － √2/4 または p = √2/4 + 1/2、数値的には、p = 0.8535533905 または p = 0.1464466094・・となる」

「と、このあたりで止まっているのね」

「p=1/2の場合は、初期条件、境界条件として、
　t=0では、f(x，t)=δ(t)、
　x=0では、∂（f，x）=0、（断熱条件）、
　x=cでは、f(x=c，t)=0、（放熱条件）、
　を課して、具体的な解を求めることができた。
　しかし、p<>1/2では、どうも様子が異なるようじゃ。
　直感的に考えて、x=0で、∂（f，x）=0、は、成り立たないような気もするしのう。
　p=1/2では、方程式を熱伝導の場合と比較して考えた。その場合、方程式は、『放物型』となる。
　境界条件も熱伝導の問題から類推した。
　pが1/2と異なる場合は、双曲型の偏微分方程式となるため、当初、拡散方程式　
　∂（f，t）=（1/2）∂（f，x，2）＋D∂（f，x）、と対比して考えていこうとしていたんじゃ。
　それが、『道中双六の問題（続々）』及び『道中双六の問題（補筆1）』じゃった。
　けれども、『道中双六の問題（補筆2）』で見たように、∂（∂（f，x），t）、の項が無視できないのではないかと考えるようになった。
　なお、∂（∂（f，x），t）をゼロと見なした場合、∂（f，x，2）をゼロと見なさないと、方程式が『楕円型』となってしまう。
　このあたりは、下記の表を参照のこと。⇒『道中双六の問題（補筆2）』。
　  ∂(∂(f, t), x)
ゼロと見なさない ゼロと見なす
∂(f, t, 2) ∂(f, t, 2)
ゼロと見なさない ゼロと見なす ゼロと見なさない ゼロと見なす 
p=0  放物型 放物型 楕円型 放物型
0<p<1/2  楕円型 双曲型 楕円型 放物型
p=1/2  楕円型 放物型 楕円型 放物型
1/2<p<1  楕円型 双曲型 楕円型 放物型
p=1  放物型 放物型 楕円型 放物型
　普通、楕円型の偏微分方程式の初期値問題は、適切な解がないと言われていることから、これは、難しい」

「えーと、仮に、2次の項を全部ゼロと見なしてしまうと、
　∂（f，t）=－q∂（f，x）、となる。ここで、q=2p－1、
　この一般解は、f=φ（x－qt）、となる。ここで、φは、任意関数。
　これは、確率密度関数の波形が速さ q=2p－1 で進むことを表している。
　だけど、ここまで、単純化してしまうと、p=1/2では、解が変化しないし、p<1/2では、振り出しより後ろには、進めないから困る」

「そうじゃな。
　その場合、揺らぎの効果をまったく無視してしまうことになるのう。
　で、やや、手詰まり感が出てきたので、もう少し、問題を広げて、次節以降で考えていきたい。
　その後、p<>1/2のケースを再検討したいと思って、課題2として挙げたのじゃ」
　目次へ戻る

課題3　対称型道中双六の問題

「今まで、考えてきた『道中双六の問題』は、振り出しから、更に後ろに戻ることは、できなかった。
　というか、それは、普通の双六では、ないからの。
　今後は、対称型の場合も考えてみよう、というわけじゃ。
　振り出しが特別な役割を果たしていることで、難しくなっていた面もあり、変えるとどのような影響があるかを考えてみよう、というのが課題3じゃ。
　で、これまでの道中双六は、『非対称型（道中双六の問題）』と呼ぶことにしよう」

「対称型の道中双六の絵を、ざっと、描いてみると、こんな感じね。
　これは、振り出しの左右に宿場数が4つずつの場合。
　ここでは、振り出しの位置をゼロとして、上がり方向に、宿場を1から4まで、下り方向に宿場－1～－4まで、としている。
　また、上がりを5、下がりを－5、と見なす。
　ま、ぶっちゃけた話、上がりを『天国』と考えれば、下がりは、『地獄』となるわね。
　つまり、対称型道中双六は、『天国と地獄』双六ね。

　
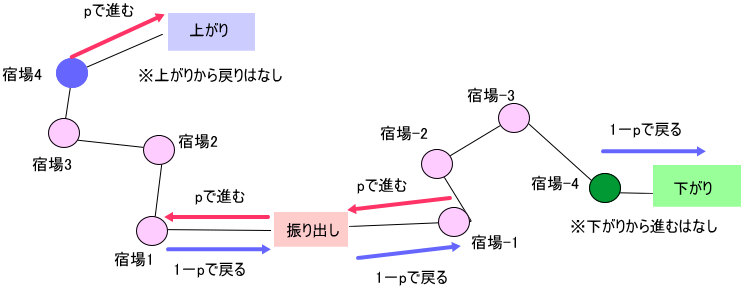
　一応、従来の非対称型の規則を踏襲して、上がりから戻ることはなく、下がりから進む（宿場－4方向）ことは、ないとした。
　こうしないと、ゲームが終わらない可能性があるからね。
　ただし、対称型では、振り出しが持っていた特別な役割は、なくなって、振り出しは、他の宿場と同じ扱いになる」

「なるほど。
　下がりから上がり方向を、進む、逆方向を、戻る、とも言うのじゃな。
　では、この問題を、課題3とすることにしよう」
　目次へ戻る

宿場数が1つずつの場合・2つずつの場合

「対称型の問題の特徴をつかむために、下図のように、最も簡単な場合を計算してみよう。

　
　ともちゃん、この場合を検討してご覧」

「例のダイアグラム（グラフ）を描いて考えてみたよ。

　
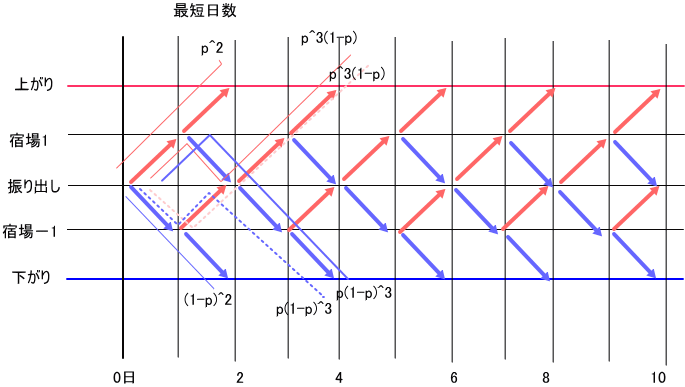
　見やすくするために、q=1－p、と置きます。
　上がる場合を考えるとすると、
　最短の2日で上がる確率は、p^2、
　4日では、2p^3 q、ここで、2倍としているのは、経路が2通りあるからね。
　以下同様に、2m＋2 で上がる確率は、2 p^2（p q）^m、（後述のようにこれは誤り）
　ここで、m=1～の整数とします」

「惜しいのう。
　そうでは、ないんだな。
　Σ上がり確率=(p^2 + ∑（m=1～∞）（2 p^(m + 2) q^m)＝2·(p － 1)/(p^2 － p + 1) － p^2 + 2、（後述のようにこれは誤り）
　同様に、下がりになる確率を考えると、これは、上の式で、pを1－pに置き換えると得られる。
　Σ下がり確率＝(1 － p)^2 + ∑(2·(1 － p)^(m + 2)· p^m,)＝－ 2·p/(p^2 － p + 1) － p^2 + 2·p + 1、（後述のようにこれは誤り）
　2つの確率の和と上がり＋下がりは、下図のグラフとなる。
　

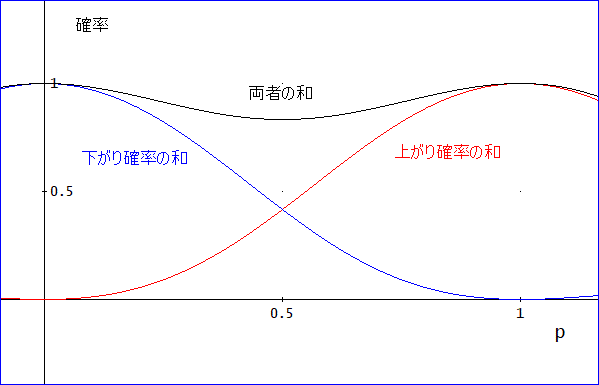
　しかし、この結果は、おかしいのじゃ」

「たしかに。
　上がりと下がりの確率の合計が1にならない。
　こいつは、どこか間違っているわ」

「m=2の場合、すなわち、2m+2＝6日で上がりに至るルートを下図で示してみよう。
※最後の振り出しから上がりへは、黒い矢印2本で代表させている。

　
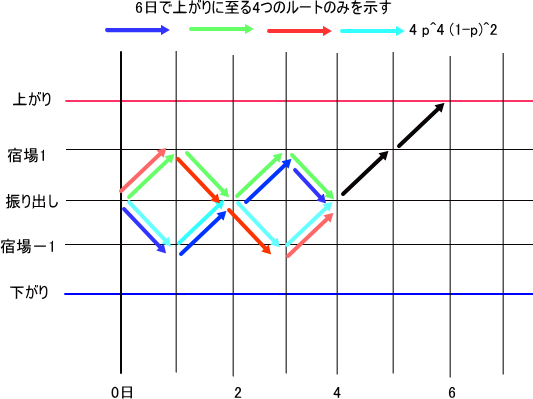
　これを見ると、はっきりすると思うが、2通りではなく、経路は、4通りあるのじゃな」

「う～ん。
　振り出しから宿場1との折り返しすることを「A」、振り出しから宿場－1との折り返しすることを「B」で模式的に表すと、
　m=1の場合は、AB または BA の2通りだったんだけど、
　m=2では、A B をそれぞれ2つずつ取り出して並べる場合なので、
　ABAB , BABA , BAAB , ABBA　と4通りできる。
　従って、一般のmでは、2つのうちから、それぞれm個ずつ取り出して並べる順列の数なので、2^m 通りとなるのね。
　2m＋2 で上がる確率は、2^m p^2（p q）^m、（m=0～）
　※m=0の場合を含めて、上式のように表すことができる。
　よって、
　Σ上がり確率=∑（m=0～∞）(（2^m p^(m + 2) q^m)＝p^2/(2·p^2 － 2·p + 1)、
　また、2m＋2 で下がりに達する確率は、2^m q^2（p q）^m、
　Σ下がり確率＝∑（m=0～∞）(2^m q^(m + 2)· p^m,)＝(p － 1)^2/(2·p^2 － 2·p + 1)、
　従って、それぞれの確率の和と両者の和の計が下のグラフのようになったわ」

　

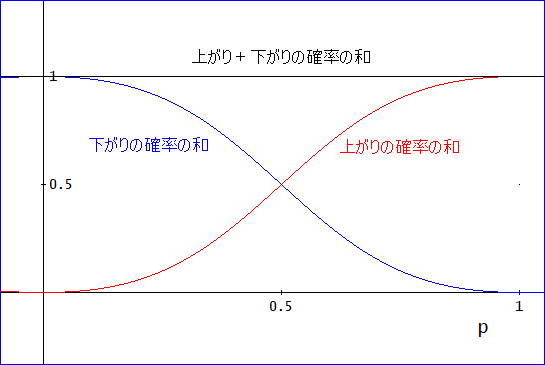
「ようできたな。
　ダイアグラムを目で見ていると、ちょっと、誤りに気がつきにくかったかも知れんな。
　確率の和をチェックしてみて分かった。
　これから、上がりまたは下がりに達する平均日数は、上がりまたは下がりの確率の和が1となることを考慮して、
　Σ（m=0～∞）（2m＋2）（上がり確率＋下がり確率）
　＝Σ（m=0～∞）（（2m＋2）×(2·p^2 － 2·p + 1)·(2·p·(1 － p))^m)＝2/(2·p^2 － 2·p + 1)、と計算できる。
　この上がりまたは下がりに達する平均日数のグラフは、下図の通りじゃ」

　
　
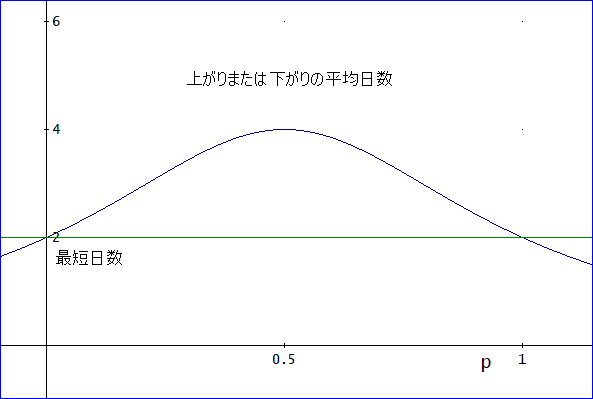
「対称型の問題らしく、p=1/2 に対して、対称となったわ。
　なんと、p=1/2の場合が平均日数が一番長くて、4日。
　この対称型双六だと、非対称型の場合と異なって、pの如何に関わらず、平均日数は、2日～4日、となるのね」

「きれいな形となったのう。
　非対称型の場合は、c=2、c=3で次のグラフのようになっていた。
　

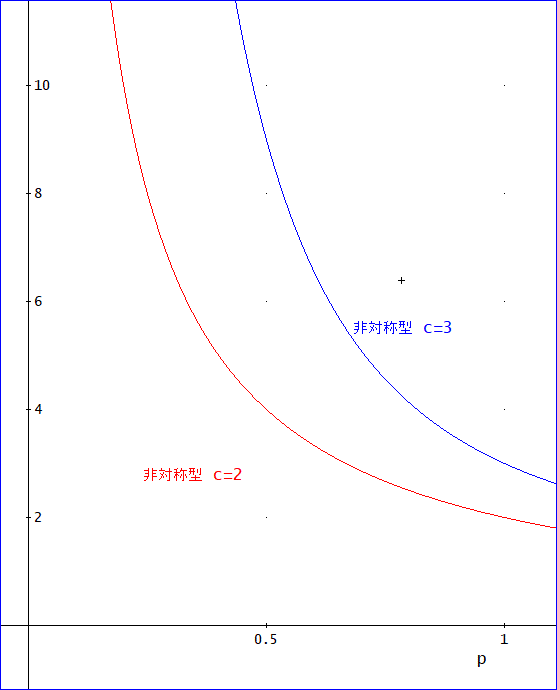
　で、ここからは、予想じゃが、非対称型では、p=1/2の場合、上がり側から振り出しを通って、下がり側に行くものと逆に下がり側から振り出しを通って、上がり側に出てくるものとが、同じ割合となるじゃろう。
　これは、振り出しが、あたかも、確率1で、上がり側から下がろうとする駒を止めて、確率1で上がり側に送り出しているのと同じことになるのではないか。
　そうすると、対称型と非対称型では、p=1/2 のケースの平均日数が同一となるのではないかと思う。
　一方、p<>1/2の場合は、非対称型とは、異なったものとなるじゃろう」

「そいつは、どうかしらね～。
　対称型で、c=3の場合について　EXCELで数値計算してみた。
　
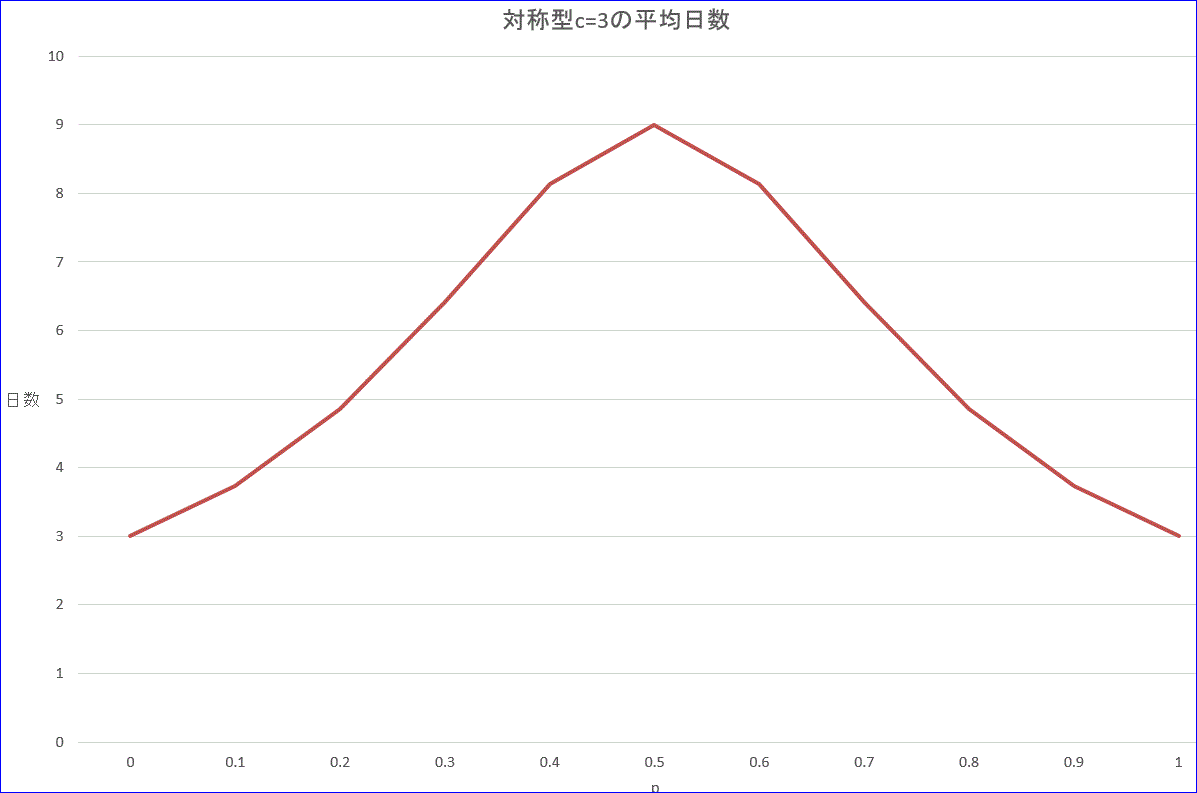
　なるほど、p=1/2の場合は、平均日数は、9となり、非対称型と同じね。
　この結果を見ると、おじぃさんの言うことも一理あるかも知れないわ」

「続く・・・、じゃな」
※　緑字の部分は、2018/1/21に追記しました。
　目次へ戻る

課題4　フィードバック回路

「だいぶ、以前じゃが、（非対称型の）道中双六の問題で、過渡現象とラプラス変換について、触れたことを覚えておるかな」

「2014年2月のご挨拶『道中双六の問題（続）』ね。
　だけど、宿場数1と2について、短く、考察しているだけで、終わってしまっていた」

「宿場数が1の場合は、演算子法に従うと、このような回路のフィルターは、像空間の変数を、sで示すと、
　exp(－s)×p×exp(－s)／（1－exp(－s)×(1－p)exp(－s)）、となる。
　これは、p×exp(－2s)／（1－(1－p)exp(－2s)）
=pe^(－2s) + pe^(－4s)(1－p) + pe^(－6s)(p－1)^2 + pe^(－8s)(1－p)^3 + pe^(－10s)(p－1)^4 + e^(－12s)(1－p)^5・・、
となるので、原空間では、入力信号をf(t)とするとき、出力信号は、
　p×f(t－2)+p(1－p)×f(t－4)+p(1－p)^2×f(t－6)+p(1－p)^3×f(t－8)+p(1－p)^4×f(t－10)＋p(1－p)^5×f(t－10)・・、
と遅延することがわかる。
下図のようじゃ」



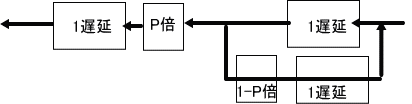
「宿場数が2の場合は、
　原空間では、p^2(1－p^2)f(t－3)＋p^2(1－p^2)f(t－5)＋p^2(1－p^2)f(t－7)＋・・、となるように考えると、
伝達関数は、p^2(1－p^2)exp(－3s)／（1－(1－p^2)exp(－2s)）でなければならないのね。
　
　
　と言う図で表される」
「ポイントとなるのは、その次の部分じゃ。
　これは、近似的ではあるが、

　
　と考えることも可能じゃろう、と指摘しているんじゃが、その後の検討をしてこなかった。
　宿場数が3以上に拡張して考えられるのかどうか、課題4として挙げておこう」
　目次へ戻る

課題5　マルコフ過程等

「はじめに、で述べた『ランダムウォーク』は、『マルコフ過程』や『拡散過程』と呼ばれる物理・数学の広い分野に含まれる。
　紙数が大幅に超過したので、関連する項目をいくつか挙げて、今後の課題5としておこう。
　・　ランダムウォーク、
　・　ランジュバン方程式、
　・　アインシュタインの関係、
　・　マルコフ連鎖、
　・　フォッカー・プランクの方程式（チャップマン・コルモゴロフの前進・後退方程式）」
　目次へ戻る

最終更新日　2018/1/20　一部追記　2018/1/21、メタタグを追加 2018/9/21、文章を微修正 2018/9/23