
新しい図表示
過渡現象
宿場数(s)が一般の場合
偏微分方程式で近似
Excelでの数値計算結果(2014/2/4、2/5追記)
終わりにあたって
 「前月の問題の続きね。
「前月の問題の続きね。
それはそうと、おじさん、体調大丈夫なの」
「ともちゃんか、いや、心配を掛けたのう。
大勢のみなさまにも、大変なお力添えをいただいた。厚く感謝申し上げます。
なかなか、元のようには復調はしないがの。
当面は、ぼつぼつと、進めていきたいと思っていますので、よろしくお願いします。
さて、2014年1月のご挨拶で、「道中双六の問題」を取り上げた。
そこでは、主として、ともちゃんが書いてくれた、図表示に基づいて書き進めた」
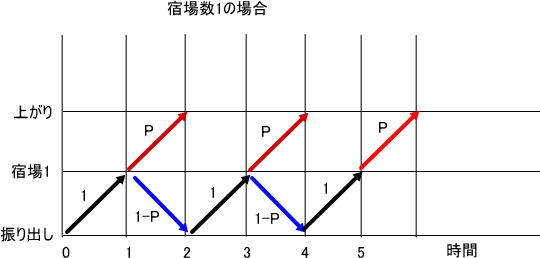
「宿場数が1の場合は、こんな感じだったわね。
そもそも、「道中双六の問題」は、 いわゆる、絵双六で、駒を振り出しから進めるんだけど、
1.駒は、振り出しから、必ず、1番目の宿場に進める。
2.駒は、各宿場で、確率Pで、次の宿場に進み、確率(1-P)で1つ戻るものとする。
3.駒が最後の宿場から上がりに進んだときは、双六上から消える。
4.駒どおしの関係は、無いものとする。
5.振り出しから、1番目の宿場まで、及び、各宿場間、並びに、最後の宿場と上がりまでの所要時間は、同一とし、1日と勘定する。
というようルールで行うと仮定したゲームで、平均何日で上がれるかを計算したいという問題ね。
それで、分かりやすいように、前回は、上の図表示を使ったの。
縦線が、振り出しから上がりまでを示していて、数字は、0が振り出し、上がりは s+1、(宿場数を s)。
また、3種類の矢印の黒は、確率1での推移、赤は、確率P、青は、確率(1-P)での推移をそれぞれ表す」
「1月は、床についていることが多かったので、いろいろと頭の中で考えてみたのじゃが、もう少し、分かりやすい図を思いついたというわけじゃ。
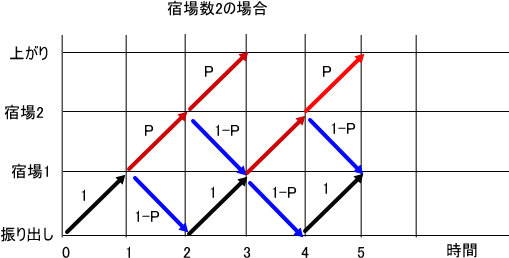
それが、上に示したような図じゃ」
「横線が、時間(振り出し、上がりを含めて、宿場間の移動に要する時間を1)で、縦軸が位置(振り出しが0、上がりがs+1)を示すという事ね。
なるほど、これだと、宿場数が一般の場合にも、煩雑にならずに構造を示せそうね」
「そうじゃろう。
次節では、一般の場合に入る前に、すこし、違った角度からこの問題を眺めてみようかの」
目次に戻る
「以下では、Pがゼロではない場合をもっぱら考えよう。
そうすると、宿場数sが、いくつであっても、時間が相当程度経過した後では、すべての駒は、上がりに到達して、盤上から、いなくなってしまう」
 「それは、そうね。
「それは、そうね。
駒の代わりに振り出しから一定時間のみ光が放射されたとして、宿場を半透明な膜と考えて透過・反射時の損失がなく、また、振り出しは、反射率が1で、上がりは、反射率がゼロであるとすれば、時間が経過した後は、すべての光は、上がりに吸収されてしまうとすれば分かりやすいかしら」
「そうじゃな。
盤上の駒の数が保存されず、すべて上がりに、吸収されてしまうので、考えている状態は、定常状態ではない。
その意味で、この道中双六の問題は、「過渡現象」を扱っていると考えられる」
「過渡現象と言えば、電気回路などの問題が思い浮かぶわね。
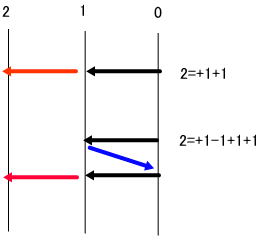
s=1で考えると、
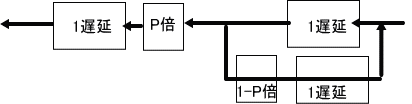
上の図のように、フィードバックがある回路になる。
演算子法に従うと、このような回路のフィルターは、像空間で、変数を、s(ここでは宿場数ではない)で示すと、
exp(-s)×p×exp(-s)/(1-exp(-s)×(1-p)exp(-s))、となる。
これは、p×exp(-2s)/(1-(1-p)exp(-2s))
=pe^(-2s) + pe^(-4s)(1-p) + pe^(-6s)(p-1)^2 + pe^(-8s)(1-p)^3 + pe^(-10s)(p-1)^4
+ e^(-12s)(1-p)^5・・、
となるので、原空間では、入力信号をf(t)とするとき、出力信号は、
p×f(t-2)+p(1-p)×f(t-4)+p(1-p)^2×f(t-6)+p(1-p)^3×f(t-8)+p(1-p)^4×f(t-10)+p(1-p)^5×f(t-10)・・、
と遅延することがわかる」
「各係数を見ると、t=2m+2として、p(1-p)^m、ここで、m=0~の整数となっている。
これは、前回に求めた、2m+2回で、上がれる確率と等しい」
「ついでに、宿場数が2の場合の伝達関数はと言うと、前回の記事を参考にして、
原空間では、p^2(1-p^2)f(t-3)+p^2(1-p^2)f(t-5)+p^2(1-p^2)f(t-7)+・・、となるように考えると、
伝達関数は、p^2(1-p^2)exp(-3s)/(1-(1-p^2)exp(-2s))でなければならない」
「確かにな。
図で表すと、

となる。
これは、近似的ではあるが、

と置き換えて考えることも可能じゃろう」
目次に戻る
「さて、いよいよ、宿場数が1以上の一般の場合を考える。
このとき、前々節に記載した図が役に立つ。
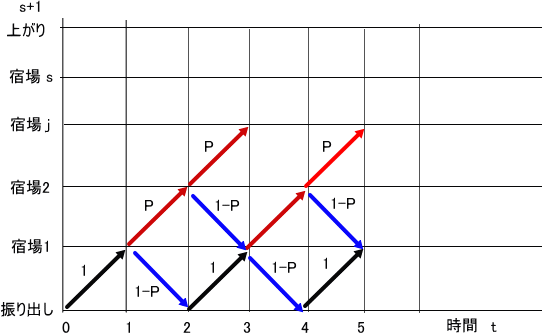
上の図は、一般のs(宿場数)の場合じゃ。
ここで、時間をtで、振り出しから上がりまでをj(0~s+1)で表す。
このとき、各交点の確率をf(j,t)とするとき、以下の式が成り立つ。
(1)f(0,0)=1
(2)t<j → f(j,t)=0
(3)j>s+1 → f(j,t)=0
(3)f(0,t)=(1-p)×f(1,t-1)
(4)f(1,t)=f(0,t-1)
(5)j<s → f(j,t)=(1-p)×f(j+1,t-1)+p×f(j-1,t-1)
(6)上記以外は、f(j,t)=p×f(j-1,t-1)」
 「じゃ、早速、DERIVEで定義してみるよ。
「じゃ、早速、DERIVEで定義してみるよ。
結構、面倒だったけど、上の図のようになった。
試しに、s=1,2,3,4,5の場合の、f(s+1,s+2m-1)をm=1~10まで計算してみた。
s=1の場合、
([p, p(1 - p), p(p - 1)^2, p(1 - p)^3, p(p - 1)^4, p(1 - p)^5, p(p - 1)^6,
p(1 - p)^7, p(p - 1)^8, p(1 - p)^9])
s=2の場合、
([p^2, p^2(p + 1)(1 - p), p^2(p + 1)^2(p - 1)^2, p^2(p + 1)^3(1 - p)^3,
p^2(p + 1)^4(p - 1)^4, p^2(p + 1)^5(1 - p)^5, p^2(p + 1)^6(p - 1)^6, p^2(p
+ 1)^7(1 - p)^7, p^2(p + 1)^8(p - 1)^8, p^2(p + 1)^9(1 - p)^9])
s=3の場合
([p^3, p^3(1 - p)(2p + 1), p^3(p - 1)^2(4p^2 + 3p + 1), p^3(1 - p)^3(2p
+ 1)(4p^2 + 2p + 1), p^3(p - 1)^4(16p^4 + 20p^3 + 13p^2 + 5p + 1), p^3(1
- p)^5(2p + 1)(4p^2 + p + 1)(4p^2 + 3p + 1), p^3(p - 1)^6(64p^6 + 112p^5
+ 104p^4 + 63p^3 + 26p^2 + 7p + 1), p^3(1 - p)^7(2p + 1)(4p^2 + 2p + 1)(16p^4
+ 16p^3 + 10p^2 + 4p + 1), p^3(p - 1)^8(4p^2 + 3p + 1)(64p^6 + 96p^5 +
84p^4 + 51p^3 + 21p^2 + 6p + 1), p^3(1 - p)^9(2p + 1)(16p^4 + 12p^3 + 9p^2
+ 3p + 1)(16p^4 + 20p^3 + 13p^2 + 5p + 1)])
s=4の場合、
([p^4, p^4(1 - p)(3p + 1), p^4(p - 1)^2(8p^2 + 4p + 1), p^4(1 - p)^3(3p
+ 1)(7p^2 + 2p + 1), p^4(p - 1)^4(55p^4 + 40p^3 + 19p^2 + 6p + 1), p^4(1
- p)^5(3p + 1)(6p^2 + 1)(8p^2 + 4p + 1), p^4(p - 1)^6(377p^6 + 354p^5 +
219p^4 + 100p^3 + 34p^2 + 8p + 1), p^4(1 - p)^7(3p + 1)(7p^2 + 2p + 1)(47p^4
+ 20p^3 + 10p^2 + 4p + 1), p^4(p - 1)^8(8p^2 + 4p + 1)(323p^6 + 210p^5
+ 132p^4 + 64p^3 + 21p^2 + 6p + 1), p^4(1 - p)^9(3p + 1)(41p^4 + 8p^3 +
9p^2 + 2p + 1)(55p^4 + 40p^3 + 19p^2 + 6p + 1)])
s=5の場合
([p^5, p^5(1 - p)(4p + 1), p^5(p - 1)^2(13p^2 + 5p + 1), p^5(1 - p)^3(40p^3
+ 19p^2 + 6p + 1), p^5(p - 1)^4(121p^4 + 66p^3 + 26p^2 + 7p + 1), p^5(1
- p)^5(364p^5 + 221p^4 + 100p^3 + 34p^2 + 8p + 1), p^5(p - 1)^6(1093p^6
+ 727p^5 + 364p^4 + 143p^3 + 43p^2 + 9p + 1), p^5(1 - p)^7(3280p^7 + 2367p^6
+ 1286p^5 + 560p^4 + 196p^3 + 53p^2 + 10p + 1), p^5(p - 1)^8(9841p^8 +
7652p^7 + 4459p^6 + 2105p^5 + 820p^4 + 260p^3 + 64p^2 + 11p + 1), p^5(1
- p)^9(29524p^9 + 24601p^8 + 15256p^7 + 7705p^6 + 3260p^5 + 1156p^4 + 336p^3
+ 76p^2 + 12p + 1)])
となるんだけど、例によって、再帰呼び出し関数は、計算に時間がかかるわね」
「二重の再帰関数じゃからな。
DERIVE de ドライブで触れたように、ベクトルを使えば、計算速度は上げられるがの。
今回は、取り上げないことにしよう」
「s=1と2は、規則的なんだけど、s=3から、式が難しくなっちゃう。
そこで、s=1から4までの、確率密度の近似和をグラフにしてみた。
和は、t=s+1~s+2m-1、(m=1~10)の範囲で計算している。
横軸は、確率 p。こんな感じ」
「予想どおりじゃが、s(宿場数)が増えると、p<1では、なかなか上がりにくくなることが分かるのう」
「でも、五十三次のs=53は、ほど遠いわ」
「一番よいのは、この確率密度関数の母関数が分かれば、上がる日数の平均値の計算はできるが、ちょっと、今は分からない」
「s=53は、大きいので、差分を微分で近似したらどうかしら?」
「そう、それが、現実的な考えじゃ」
目次に戻る
「時間をtで、位置をxで表すことにしよう。
基本となるのは、f(x,t)=(1-p)×f(x+1,t-1)+p×f(x-1,t-1)じゃな」
 「変数の範囲は、t=0~∞、x=0~s+1、となるわね。
「変数の範囲は、t=0~∞、x=0~s+1、となるわね。
上式で、tをt+1に替えて、f(x,t+1)=(1-p)×f(x+1,t)+p×f(x-1,t)、
1を微少量と考えて、
左辺は、f(x,t)+∂(f,t,1)+(1/2)∂(f,t,2)+・・、
また、右辺の第1項は、(1-p)(f(x,t)+∂(f,x,1)+(1/2)∂(f,x,2)+・・)、
同様に第2項は、p(f(x,t)-∂(f,x,1)+(1/2)∂(f,x,2)+・・)、
となるので、
(1-2p)∂(f,x,1)-∂(f,t,1)+(1/2)(∂(f,x,2)-∂(f,t,2))≒0、
ここで、∂(f,x,2)などは、f(x,t)をxで2回偏微分していることを表す」
「まあ、そういうことかな。
fのtに関する変化率が小さいとすれば、更に、
(1-2p)∂(f,x,1)-∂(f,t,1)+(1/2)∂(f,x,2)≒0
移項して、
∂(f,t,1)≒(1-2p)∂(f,x,1)+(1/2)∂(f,x,2)、
初期条件、境界条件は、難しいが、大まかに、f(x,x)=p^x、
f(x,0)≒δ(x) 、ここで、δ(x)は、ディラックのデルタ関数。
f(x,x)=p^x、ただし、x<s+1
f(x,t=∞)→0 などとなると思う。
今回は、時間切れじゃったな」
「でも、sが一般の場合の解決の糸口が見えてきたわ」
※青字の式が誤っていましたので、2014/2/3に修正しました。
※取り消し線部分は、2014/2/7に修正しました。
※1次元の熱伝導、拡散方程式等との対比を念頭に差分の近似式を2014/2/15にあらためました。
これにより、p≒1の場合は、∂(f,t,1)≒-∂(f,x,1)、ですが、これは、g(x)=f(x,0)と置いたときに、f(x,t)=g(x-t)が近似解となることを示します。
これは、t=0のときのg(x)が速度1で進行することを意味します。
目次に戻る
 「Excelで、道中双六の数値計算をやってみたよ。
「Excelで、道中双六の数値計算をやってみたよ。
宿場数が、s=5とs=53の場合を、第1節の表を作る方法で計算し、振り出しから上がりまでの平均日数を計算したところ、下の表のようになった。
ただし、下の表では、平均上がり日数を最短日数で除したものを載せている。
例えば、s=5、p=0.2では、倍率568.7は、実日数では、約3412日を6で割ったものなの」
| S=5 | S=53 | S=5 | S=53 | |
| P | 平均日数/最短日数 | LOG10(平均日数/最短日数) | ||
| 0.1 | ||||
| 0.2 | 568.7 | 2.754883228 | ||
| 0.3 | 67.67 | 1.830396176 | ||
| 0.4 | 15.78 | 1.198106999 | ||
| 0.5 | 6 | 53.56 | 0.77815125 | 1.728840568 |
| 0.6 | 3.18 | 4.77 | 0.50242712 | 0.678518379 |
| 0.7 | 2.065 | 2.45 | 0.314920056 | 0.389166084 |
| 0.8 | 1.519 | 1.65 | 0.181557774 | 0.217483944 |
| 0.9 | 1.203 | 1.24 | 0.080265627 | 0.093421685 |
| 1 | 1 | 1 | 0 | 0 |
「これは、労作じゃな。
いや、珍重、珍重。
どれどれ、s=53が、いわゆる五十三次の場合じゃな。
確率の和も検証してみたのかの」
「ΣPが0.98以上の場合のみ、表にしてあります。
だから、s=5で、p=0.1では、約16000個の和をとっても、ΣPが0.1程度にしかならないため、表に載せていないのね。
同じように、s=53では、p=0.5で、ΣP≒0.998・・、であるんだけど、p=0.4では、4×10^-7程度にしかならないから、カット」
「グラフがこれかの。
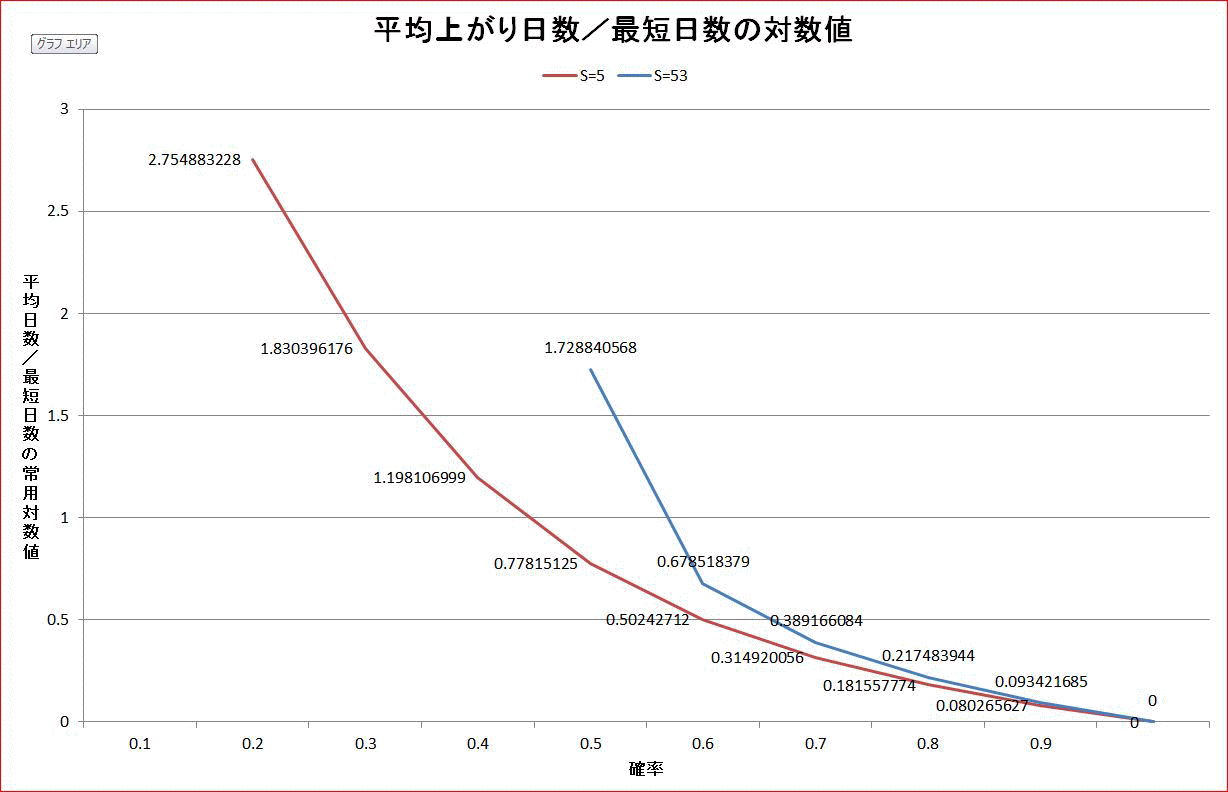
p=1/2の場合は、平均上がり日数が、s=5で、最短日数(s+1=6)の6倍、s=53で、53.5倍と、それぞれ、概ね s+1倍になっている。
前回の記事で厳密に計算した結果でも、p=1/2の場合は、s=1で、2倍、s=2で、3倍、と同一の傾向じゃ。
これらから推測すると、特に、p=1/2の場合、sの如何に関わらず、平均上がり日数は、最短日数の約s+1倍であると言えるのではないか?」
「前節の偏微分方程式も、p=1/2では、簡単になるので、そのあたりにも何か秘密がありそうね」
「物理的な描像としては、宿場数sの場合、振り出しから上がりまでの間に、s+1個の小部屋があるが、時間がs日経過後、p=1/2の時は、ほぼ、すべての小部屋に均等に入っていると考えられるのではないか。
一方、p=1の場合は、短時間に一度に出発した場合を考えてみれば分かるように、どれか1つの小部屋にしか存在しないので、1日ごとに一団となって一つ先の小部屋に進む。
最後の小部屋、これは、s個目の宿場と上がりとの間じゃが、ここに入ると、pの如何に関わらず、次は、上がることになる。
p=1の場合は、それは、s+1日後に一斉に起こり、これが最短時間じゃが、p=1/2のときは、駒がs+1個の小部屋に分散しているため、1日毎に上がる駒数は、1/(s+1)となる。
従って、平均上がり日数/最短日数は、この逆数となり、s+1倍になるという景色が思い浮かぶのう」
「なるほどね。
簡単に言えば、駒の平均の速さが、p=1/2のときは、p=1の時の速さの 1/(s+1)になるということか。
ま、感覚的には、分かる気がするけど」
※青字部分は、2014/2/5に追記しました。
※青字色の部分の取り消し線は、2014/2/6に施しました。
なぜならば、p=1/2で、s=53の場合のExcelでの数値計算結果を再確認したところ、t=s+1=54における、f(x,54)は、x=0~54の間で、均一とは言えず、xが0に近いほど、f(x,54)が1に近くなっており、0=<
x <=25の範囲のf(x,54)の和は、0.99を超えていました。
目次に戻る
今回もご覧いただき、ありがとうございました。
本年、2014年4月9日に、いよいよ、Windows XPとOffice 2003 に対するマイクロソフト社のサポートが終了を迎えます。
それまでに3ヶ月となったわけです。Office 2002までのサポートは、すでに終了しています。
サポート終了後、インターネットに接続して利用するパソコンでは、セキュリティが厳しい状態になります。
Windows 7、または、Windows 8、Windows 8.1 搭載のパソコンに買い換えましょう。もはや、考えている時間は、ありません。
特に、Windows 7のプリインストールパソコンは、量販店では、既に販売されておりませんので、通販サイト等を利用する必要があります。年度末が近づくとこれらは、品薄となり得ますので、早めに対処する必要があるでしょう。(参考URL:http://www.nikkeibp.co.jp/xp2014/)
なお、当教室でも、Office2003関係コースの新規受講受付を2013/12末で終了いたしました。
ご了承下さいますようお願い申し上げます。
では、次回も、また、本欄で元気にお会いできますことを願っています。
目次に戻る
作成 2014/2/1、目次を追加 2019/5/5