
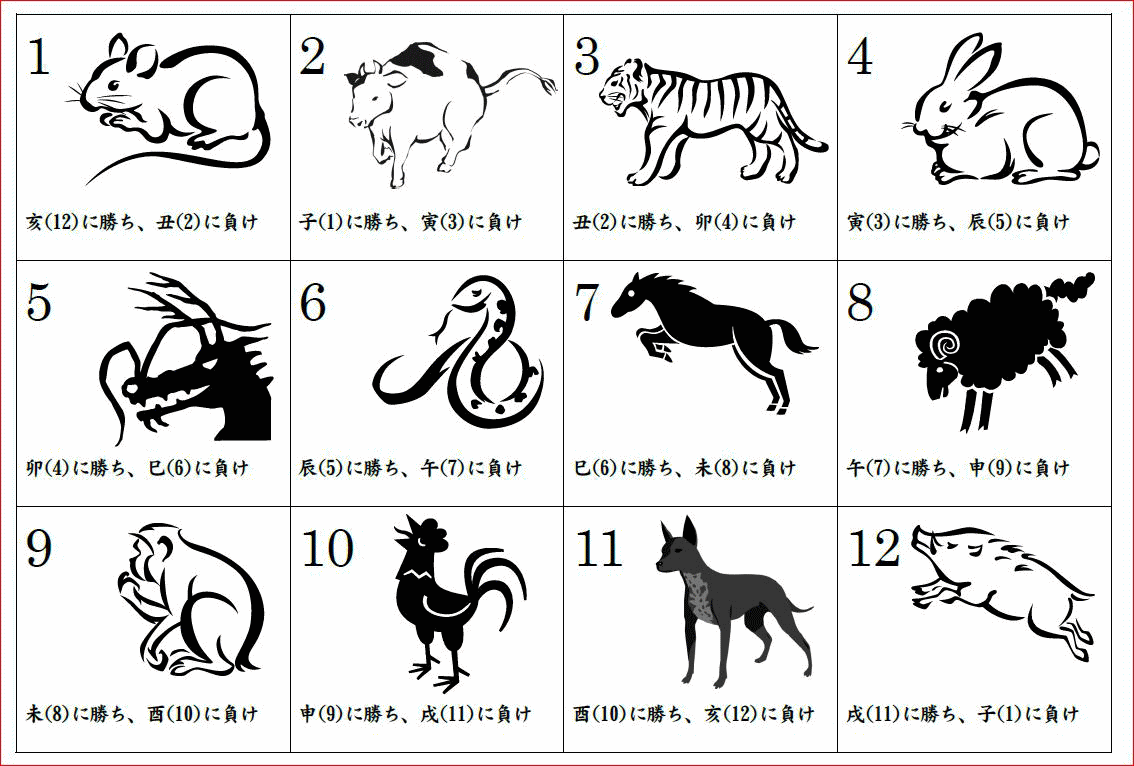
犬に「お手」とは?
三すくみ
四すくみ・五すくみ
球磨拳
『あいこ』の確率
平均試行回数
平均試行回数のばらつきと99%の範囲
確率密度関数のグラフ
可能なゲームの組合せの数(1)(三すくみ、四すくみ)
可能なゲームの組合せの数(2)(五すくみの場合のその1)
可能なゲームの組合せの数(2)(五すくみの場合のその2)
可能なゲームの組合せの数(予想とシミュレーション)
組合せ数が予想とシミュレーションで食い違う理由(2013/1/10~1/14 追記)
干支拳カード(おまけ)
終わりにあたって
『なぜ犬にお手をさせるの?』は、テレビ東京の金曜日の『所さんの学校では教えてくれないそこんトコロ!』で2012年12月27日(木)放送分に取り上げられた疑問です。
恥ずかしながら、私は、これまで一度も不思議に思わなかったですね。
番組を見逃された方は、同番組のホームページに概要が掲載されていますので、ぜひ、ご覧下さい。
http://www.tv-tokyo.co.jp/sokontokoro/
さて、簡単に書きますと、犬の祖先であるオオカミは、自分より上位のものへの服従の印として、足裏を見せるという習性をもっているそうです。
なぜ、足裏なのかというと、オオカミにとって足は、大事な部分であり、その足裏というのは、柔らかい肉球であり、それを相手に見せることで、相手に敵意のないことを示し服従する意志を表す行為のようです。犬も、また、その習性をもっているため、訓練してお手をさせることで、その人の言いつけをより守るようにする意味があるとのことでした。
まったく驚きですね、このような疑問こそ、本当の疑問です。素晴らしい。
目次に戻る
 「あけましておめでとうございます。」
「あけましておめでとうございます。」
「おー。ともちゃんか。
おめでとう」
「年賀状、ありがとうございました。おじさん。
でも『干支拳』って、どこでやっている、じゃんけんなの?」
「いや、どこもやっておらんと思うな。たぶん」
「じゃ、おじさんは、熊本県の人吉市周辺で行われているっていう『球磨拳』からヒントをもらって、干支拳を考えたのね」
「そう思うじゃろう。
ところが、そうではないんじゃ。
きっかけは、例の新党騒動じゃな。
ほれ、当時の野田総理の『そのうちの解散』により、年末総選挙となったが、新党ブームで、15政党もあったんじゃな。
もっとも、公示前後に、12に数が減った。しかし、異例というか、異様に多い。
まるで『三すくみ』に似ておるんじゃが、今回は、それ以上だと思って、『四すくみ』や『五すくみ』に拡張して考えてみたんだがな」
「その三すくみの由来だけど。
年賀状の一口メモに載っているように、蛇と蛙は、わかるけど、なぜ、『ナメクジ』が出てくるんでしょう?」
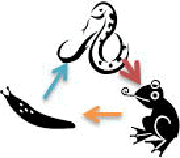 「関尹子(かんいし:中国古代の周の伝説上の人物)に曰く、『なめくじ→蛇→かえる→なめくじのように、三者が互いに牽制し合って、いずれも自由に行動できないこと』を三竦みという。(広辞苑)というものじゃな。
「関尹子(かんいし:中国古代の周の伝説上の人物)に曰く、『なめくじ→蛇→かえる→なめくじのように、三者が互いに牽制し合って、いずれも自由に行動できないこと』を三竦みという。(広辞苑)というものじゃな。
確かに、ヘビとカエルは、一般には、優劣の関係にあるが、ナメクジがヘビよりも優位というのが分からんな」
「でしょう、でしょう。
所さんのそこんトコロに、聞いてみたい疑問よね」
「そこで、グーグルで検索してみたんじゃ。
どうも、原典の中国語の『螂蛆』を『ナメクジ』と解釈したのじゃが、本来は、『ムカデ』のことらしい」
「なるほど。
ムカデなら、毒を持っているので、ヘビが嫌うのは、納得がいくけど」
「藤原審爾氏の『大妖怪』(文藝春秋社:昭和53年)に『怪異因幡大百足』という小説が収録されていて、大百足と大蛇との死闘が取り上げられておるの。
これは、氏が中国の故事に想を得たものかも知らん」
「でも、そのムカデとナメクジを取り違えったっていう江戸時代の人もさぁ、疑問に思わなかったのかしらね」
「そのあたりは、分からんな~。
ナメクジは、日本では、漢字の『蛞蝓』を当てているが、さっきの『螂蛆』とは、違うものな」
目次に戻る
「ま、ナメクジの疑問は、これくらいにして、三すくみから、四すくみなどに移ろう。
『じゃんけん』は、石(グウ)→はさみ(チョキ)→紙(パー)→石、でやはり、三すくみ。
ちなみに、じゃんけんの語源は、「石拳」または「両拳」からと言われている。同じものの場合は、「あいこ」でしょ、とやりなおし、じゃな。
そこで、四すくみでは、どうか、考えたんじゃ」
 「なるほど。
「なるほど。
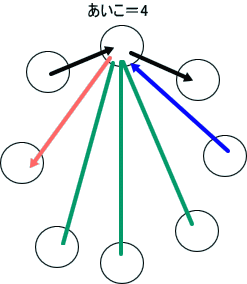
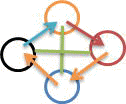 四すくみを図にすると、左上の図のようになる。
四すくみを図にすると、左上の図のようになる。
ここで、矢印は、優劣を、緑の線は、対等関係(あいこ)を表すということね」
「そうじゃ。4つのものが対等になるためには、隣同士以外のものとは、『あいこ』にしないとならないのう」
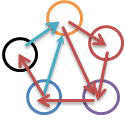 「だけど、五すくみでは、2とおりが考えられるという訳ね」
「だけど、五すくみでは、2とおりが考えられるという訳ね」
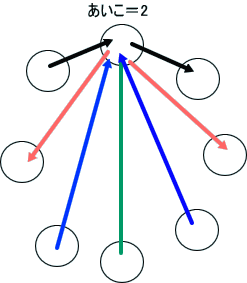
「左中図は、五すくみでも、自分以外とのあいこをすべてなくした場合じゃな。
三すくみのように、自分自身以外とのあいこがないものを、仮に『○○すくみ』と狭く定義すると、四すくみは、すくみではなくて、五すくみが三すくみの次のものと言えるかも知らん。もっとも、今回は、隣同士以外との関係が、あいことなるものも、すべて、『○○すくみ』と考えることにする。
ここで、左中図のような方法で『じゃんけん』をすると、自分自身以外はあいことならないので、『あいこ』となる確率は、1/5となる。
なお、注意しておくと、左中図では、一番上の黄色い丸だけが、他の丸と優劣関係を持つように描いてあるが、その他の丸については、煩雑なため、省略しているので、その他の丸も他の丸との間で優劣関係にあるようにする必要がある。このとき、『優』を出ていく矢印として+1点、『劣』を入ってくる矢印として、-1点、自分に対しては、ゼロ点と勘定するとき、5つの丸について、それぞれ、点数の合計がゼロとなるように優劣関係を作ることが基本じゃ」
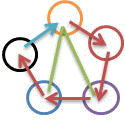 「五すくみのもう一つの場合が、左下の図ね」
「五すくみのもう一つの場合が、左下の図ね」
「この場合は、隣同士以外との関係は、すべて対等(あいこ)とした時じゃ」
「これでも、5つのものは、全体として平等な訳ね。あいこ、となる確率は、3/5と大きくなる」
「実は、この辺まで、考えてから、じゃんけんについて、インターネットで調べて見たんじゃな。
すると、思いがけなく、『球磨拳』なるものを検索してしまったということじゃ」
目次に戻る
 「球磨拳は、六すくみだった」
「球磨拳は、六すくみだった」
「そうなんじゃ。
じゃんけんのように、3種類ならともかく、4種類、5種類の手のかたちを作るのは、難しかろうと思っていたら、球磨拳なるものは、6種類じゃによって、驚いたんだがな」
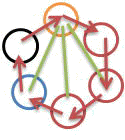 「六すくみの場合は、あいこの数によって、やはり、2とおりの場合が考えられるけど、熊本県人吉市周辺で行われている『球磨拳』は、左上図のように、隣同士以外は、『あいこ』なのね」
「六すくみの場合は、あいこの数によって、やはり、2とおりの場合が考えられるけど、熊本県人吉市周辺で行われている『球磨拳』は、左上図のように、隣同士以外は、『あいこ』なのね」
「そのようじゃな。
丸の部分は、実際は、異なる手のかたちを表すが、球磨拳では、数字(ウィキによると、0から5までとのこと)を割り当てて、自分の方が相手より1つ大きい時は勝ち、相手より1つ少ないときは負け。それ以外は、あいこ、となる。
ただし、これでは、常に5を出した方が勝ちなので、0には、5が負けるとすると、平等になるのじゃな」
「熊本というと、『くまモン』という、ゆるキャラが有名ね。
その『くまモン』のホームページでも、球磨拳が紹介されているわよ。
それが、こちら。http://kumamon-official.jp/
この中で、くまモンが球磨拳体験した、みたいな記事があった」
「いやー。くまモン君、おどろきのスケジュールですな。
http://kumamon-official.jp/category/hitoyoshi-kuma/page/5
上のリンクに、くまモンが、球磨郡の多良木町で行われた、『キッズくま拳大会』に参加した様子がブログ形式で報告されているのう」
「なんか、ほんと、癒やされる、キャラですね」
「まったくな。
しかし、球磨拳が、熊本県の一部に残るというのも、不思議じゃな。
大人の大会もあって、勝負に夢中になると、焼酎の飲み方も早くなるそうじゃ。
あいこが多いからかもしれんな」
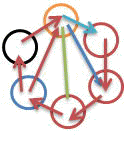 「あいこを減らすと、左下図のようになるのね。
「あいこを減らすと、左下図のようになるのね。
この場合は、あいこの確率は、2/6=1/3と普通のじゃんけんと同じとなる」
「ウィキによれば、球磨拳を簡素化したのが、普通のじゃんけんだそうな。
なお、あいこの確率は、次のように考えるとわかりやすいじゃろう。
たとえば、左下図の中央上の黄色の丸に注目するとき、
そこから、線が何本出ているかが分母になる。この場合は、自分自身への線が省略されているので、それを忘れずに入れると、6となる。
次に、その中で、緑の線の数はというと、自分への線も勘定して、2じゃ。そこで、あいことなる確率は、2/6=1/3という訳じゃ」
「球磨拳の場合は、左上図で、緑が3本+1本で4なので、あいことなる確率は、4/6=2/3ということね。
球磨拳のあいことなる確率は、2/3で、普通のじゃんけんの1/3の2倍もあり、あいことなる回数が多くなるためか、みなさん、熱くなってますね」
「ユーチューブにも大会の模様がアップされておるようじゃ」
目次に戻る
「2nすくみの場合を考える。ここで、n>1なる自然数とする。
線の総数は、自分の分も含めて、2nであり、球磨拳のように、『あいこ』がもっとも多い方を『その1』とすれば、あいことならないのは、隣同士の2本だけなので、緑の線の数は、2n-2となり、あいことなる確率(以下、p)は、p=(2n-2)/2n=1-(1/n)となる」
 「そうすると、あいこが極力少なくなるようにした場合を『その2』とすれば、p=2/2n=1/nとなるわ」
「そうすると、あいこが極力少なくなるようにした場合を『その2』とすれば、p=2/2n=1/nとなるわ」
「うん、そうじゃな。
nが4以上の場合は、その1とその2の中間の場合もある。
すなわち、あいこにできる線の合計は、2n-2-1=2n-3。(自分の分は、必然的に、あいことなる)
ここで、これらを半分ずつに分ける(優劣の数をそろえるため)と、奇数のため、1本だけは、あいこ、とせざるを得ない。
このとき、あいこの数をコントロールできるのは、2n-3-1=2n-4の1/2である、n-2本となる。(半分だけ考えればよい。残りは、同数に決まる)
n-2本のうち、あいこの数だけに注目すると、すべてあいこでない~すべてあいことするまでの数は、0~n-2までのn-1とおりある。
ちなみに、n=3のときは、2とおりで、これは、すでに前節に記載した場合じゃな」
「そうすると、n=4のときは、3とおりとなって、『その1』と『その2』の間の場合があるということになるわね」
「そうじゃな。以下が、n=4の場合(八すくみ)の場合じゃ。
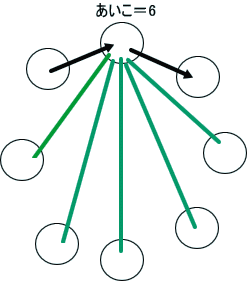
あいこ6の場合が、あいこの数がもっとも多くする場合じゃ。
あいこの確率は、p=6/8=3/4。『その1」に相当。
あいこ4の場合は、p=4/8=1/2。中間の場合。
あいこ2の場合は、p=2/8=1/4。『その2』に相当」
「こいつを一般的に、書くと、あいこの数は、k=0~n-2の2倍に半端の分と自分自身の分としてそれぞれ1を加えた、2k+2本となる。
| n | 2n | k=0~n-2 | あいこの数(2k+2) | あいこの確率 | 備考 |
| 2 | 4 | 0~0 | 2 | 1/2 | |
| 3 | 6 | 0~1 | 2、4 | 1/3、2/3 | 球磨拳 |
| 4 | 8 | 0~2 | 2、4、6 | 1/4、2/4、3/4 | |
| 5 | 10 | 0~3 | 2、4、6、8 | 1/5、2/5、3/5、4/5 | |
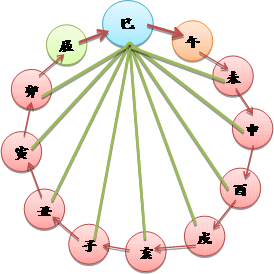
| 6 | 12 | 0~4 | 2、4、6、8、10 | 1/6、2/6、3/6、4/6、5/6 | 干支拳 |
| 7 | 14 | 0~5 | 2、4、6、8、10、12 | 1/7、2/7、3/7、4/7、5/7、6/7 |
従って、上の表のように、一般に、あいことなる確率は、p=(k+1)/n、
ただし、ここで、k=0~n-2を動くものとする」
「一つ、二つ注意しておく必要がある。
一つは、いまは、あいこの「数」だけに注目しているので、あいことする相手や優劣の関係は無視していることじゃ。
たとえば、あいこ4の場合で、青矢印と赤矢印の入れ替えや緑と矢印との入れ替えでも、別のかたちの関係が出来るのじゃが、その違いを無視していることじゃ。
二つ目は、各丸印の入れ替えも無視していることじゃ」
「丸印の入れ替えって?」
「2n個の○は、本来、グー、チョキ、パーなどのそれぞれ異なるものなので、一般に、(2n-1)!とおりの並べ方があるということじゃ」
「普通のじゃんけんでは、グー→チョキ→パーの他に、グー→パー→チョキがあるということね」
「そうじゃ。
こういったものを、一般には、ゲームルールとも言うがの。
2nあるいは2n-1をまとめて、Nで表せば、回転して、同じ並びとなるものは、N通りあるので、N個の順列の数である N!をNで割った、(N-1)!通りの丸の並べ方があるということじゃな」
「次は、じゃんけんのように、2n-1すくみの場合ね。ここで、n>1の自然数とする。
さっきの場合と同様に考えると、こんどは、半端が無いので、2n-1本のうち、隣同士と自分の分のみを引いた、2n-1-3=2n-4の半分である、n-2本がコントロール可能となる。
ちなみに、普通のじゃんけんの場合は、n=2(2n-1=3すくみ)なので、コントロール可能な本数(n-2=0)は、ゼロである。
n=3の時は、五すくみの場合で、制御可能な線の数は、1本なので、それを、あいことするか、しないか(優または劣)の2とおりとなる。
n=4の時は、七すくみの場合で、制御可能な線の数は、2本なので、あいこの数を2、1、0の3とおりに選ぶことが出来るということね」
「やはり表にしてみると、次のようになる。
あいこの数は、一般的に、k=0~n-2の2倍に自分自身の分の1を加えた、2k+1本となる」
「従って、あいことなる確率は、p=(2k+1)/(2n-1)、ここで、k=0~n-2となるわけ」
| n | 2n-1 | k=0~n-2 | あいこの数(2k+1) | あいこの確率 | 備考 |
| 2 | 3 | 0~0 | 1 | 1/3 | 普通のじゃんけん |
| 3 | 5 | 0~1 | 1、3 | 1/5、3/5 | |
| 4 | 7 | 0~2 | 1、3、5 | 1/7、3/7、5/7 | |
| 5 | 9 | 0~3 | 1、3、5、7 | 1/9、3/9、5/9、7/9 | |
| 6 | 11 | 0~4 | 1、3、5、7、9 | 1/11、3/11、5/11、7/11、9/11、 | |
| 7 | 13 | 0~5 | 1、3、5、7、9、11 | 1/13、3/13、5/13、7/13、9/13、11/13 |
「ここからは、一般に、あいことなる確率が、pの『じゃんけん』を考えよう。
対戦する人数は、2人とする。
このとき、両者が、完全にランダムに手を出す場合に、勝敗が決まるまでの回数の平均を、『平均試行回数』と呼ぶことにする。
では、ともちゃん。この回数を求めてご覧」

 「えーと。
「えーと。
あいこをゼロで、勝負がつくのを1で表すとき、ゼロは、確率pで現れ、1は、1-pで現れることになる。
これは、コインの表裏や赤白のボールで考えてもいいけどさ。
さて、k番目に、初めて、1が出る確率f(k)は、k-1のゼロが続いてからk番目に1が出るので、
f(k)=p^(k-1)×(1-p)である。ここで、k=1~∞。
従って、n番目までの平均試行回数は、Σ(k=1~n)(k×f(k))=p^n(n(p - 1) - 1)/(1 - p) - 1/(p - 1))であり、
n→∞の極限をとると、平均試行回数は、1/(1-p)となる」
「よくできましたな。
ちなみに、普通のじゃんけんでは、p=1/3なので、平均試行回数は、1.5回となる」
「球磨拳では、p=2/3なので、平均試行回数は、3回。
干支拳では、p=5/6なので、6回となると言う訳ね」
目次に戻る
「では、ついでに分散と標準偏差も求めてみよう。
分散=Σ(k=1~n)((k-1/(1-p))^2×f(k))→p/(1-p)^2、n→∞。
従って、標準偏差は、(√p)/(1-p)となる」
 「さらに、確率の累積密度関数は、Σ(k=1~n)f(k)=1-p^nとなるので、年賀状にあるように、この値が0.99となるnを求めてみると、
「さらに、確率の累積密度関数は、Σ(k=1~n)f(k)=1-p^nとなるので、年賀状にあるように、この値が0.99となるnを求めてみると、
n=2LN(10)/LN(1/p)となる。
表にしてみると、次のようになるわ」
| すくみの数 | あいこの数 | あいこの確率 | 平均試行回数 | 標準偏差 | 99%のn | 備考 |
| 3 | 1 | 1/3 | 1.5回 | √3/2≒0.86 | 4.19 | 普通のじゃんけん |
| 4 | 2 | 2/4=1/2 | 2回 | √2≒1.41 | 6.64 | 四すくみ |
| 5 | 1 | 1/5 | 1.25回 | √5/4≒0.56 | 2.86 | 五すくみ |
| 5 | 3 | 3/5 | 2.5回 | √15/2≒1.94 | 9.02 | 同上 |
| 6 | 2 | 2/6=1/3 | 1.5回 | √3/2≒0.86 | 4.19 | 六すくみ |
| 6 | 4 | 4/6=2/3 | 3回 | √2≒1.41 | 11.35 | 球磨拳 |
| 7 | 1 | 1/7 | 7/6≒1.17回 | √7/6≒0.44 | 2.37 | 七すくみ |
| 7 | 3 | 3/7 | 1.75回 | √21/4≒1.15 | 5.43 | 同上 |
| 7 | 5 | 5/7 | 3.5回 | √35/2≒2.96 | 13.69 | 同上 |
| 8 | 2 | 2/8=1/4 | 4/3≒1.33回 | 2/3≒0.67 | 3.32 | 八すくみ |
| 8 | 4 | 4/8=1/2 | 2回 | √2≒1.41 | 6.64 | 同上 |
| 8 | 6 | 6/8=3/4 | 4回 | 2√3≒3.46 | 16.00 | 同上 |
| 9 | 1 | 1/9 | 1.125回 | 0.375 | 2.10 | 九すくみ |
| 9 | 3 | 3/9=1/3 | 1.5回 | √3/2≒0.87 | 4.19 | 同上 |
| 9 | 5 | 5/9 | 2.25回 | 3√5/4≒1.68 | 7.83 | 同上 |
| 9 | 7 | 7/9 | 4.5回 | 3√7/2≒3.97 | 18.32 | 同上 |
| 10 | 2 | 2/10=1/5 | 1.25回 | √5/4≒0.56 | 2.86 | 十すくみ |
| 10 | 4 | 4/10=2/5 | 5/3≒1.67回 | √10/3≒1.05 | 5.02 | 同上 |
| 10 | 6 | 6/10=3/5 | 2.5回 | √15/2≒1.94 | 9.02 | 同上 |
| 10 | 8 | 8/10=4/5 | 5回 | 2√5≒4.48 | 20.64 | 同上 |
| 11 | 1 | 1/11 | 1.1回 | √11/10≒0.33 | 1.92 | 十一すくみ |
| 11 | 3 | 3/11 | 1.375回 | √33/8≒0.72 | 3.54 | 同上 |
| 11 | 5 | 5/11 | 11/6≒1.83回 | √55/6≒1.24 | 5.84 | 同上 |
| 11 | 7 | 7/11 | 2.75回 | √77/4≒2.19 | 10.19 | 同上 |
| 11 | 9 | 9/11 | 5.5回 | 3√11/2≒4.97 | 22.95 | 同上 |
| 12 | 2 | 2/12=1/6 | 1.2回 | √6/5≒0.49 | 2.57 | 十二すくみ |
| 12 | 4 | 4/12=1/3 | 1.5回 | √3/2≒0.86 | 4.19 | 同上 |
| 12 | 6 | 6/12=1/2 | 2回 | √2≒1.41 | 6.64 | 同上 |
| 12 | 8 | 8/12=2/3 | 3回 | √6≒2.45 | 11.35 | 同上 |
| 12 | 10 | 10/12=5/6 | 6回 | √30≒5.48 | 25.26 | 干支拳 |
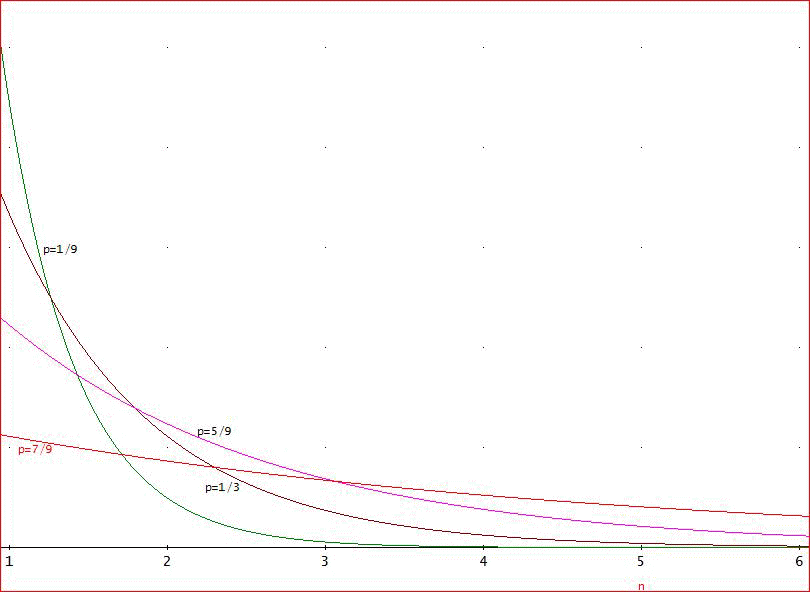
「代表的な例の確率密度関数f(n)のグラフを載せておこうかな」
下のグラフは、あいこの確率が、1/9、1/3(普通のじゃんけん)、5/9、7/9の場合じゃ。
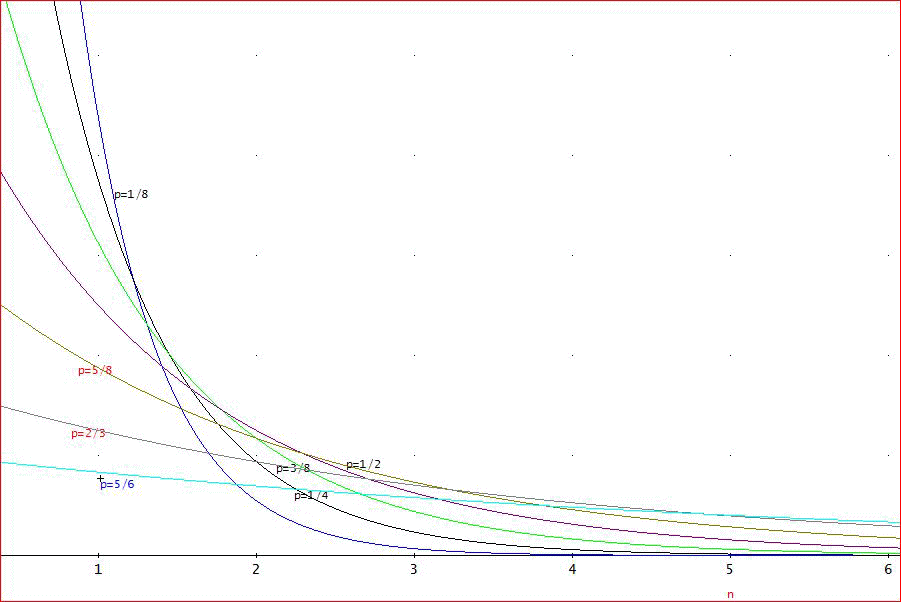
次に、下のグラフは、あいこの確率が、1/8、1/4、3/8、1/2、5/8、2/3(球磨拳)、5/6(干支拳)の場合じゃな」
 「じゃ、わたしは、累積密度関数の代表的なグラフを描くよ。
「じゃ、わたしは、累積密度関数の代表的なグラフを描くよ。
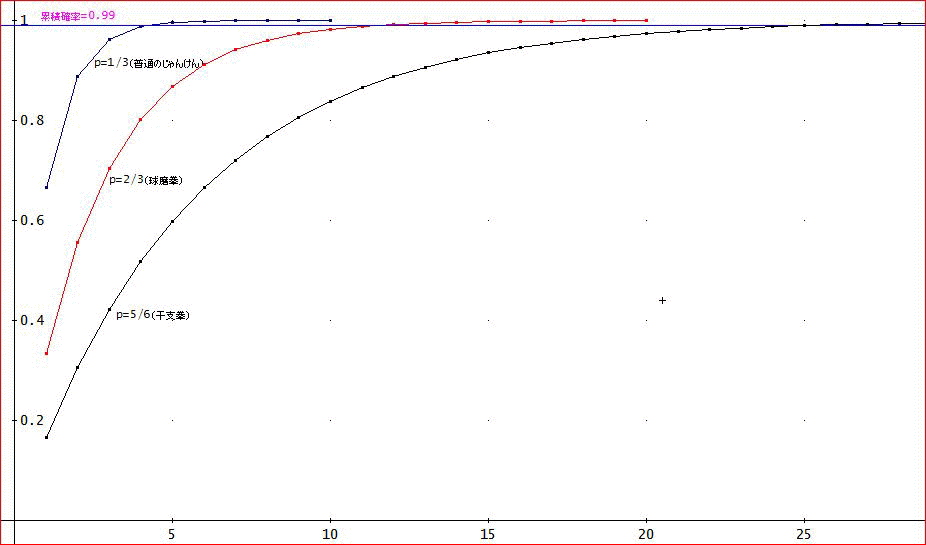
普通のじゃんけん(あいこの確率=1/3)、球磨拳(同p=2/3)、干支拳(同p=5/6)の場合ね。
累積確率が0.99の線を横に引いてあるので、大体分かると思うけど、99%ラインと交わる点のnは、普通のじゃんけんが約4回、球磨拳が約11回、干支拳が約25回であることが見て取れるわ」
目次に戻る
「これまで、丸印の優劣関係やあいこ関係などは、あいこの数たげに注目してきたが、もし、丸印同士の個性も区別すると、どのくらいの組合せが考えられるかのう」
 「可能なゲームの組合せの数のことね。
「可能なゲームの組合せの数のことね。
三すくみの場合は、さっき出てきたとおり、2とおりね。
四すくみの場合は、6とおりではないかと思うわ」
「今、個別の丸印をi(1からn。ただし、n>=3)で表し、お互いの関係をr(i,j)で示すことにする。
このr(i,j)は、iがjに対して、「優」の場合は、「+1」、逆に、iがjに対して「劣」の場合は、「-1」、あいこのばあいは、「0」と決めよう。
このとき、容易に、r(i,j)=-r(j,I)、また、r(i,i)=0である。
また、互いが対等であるためには、Σ(j=1~n)r(i,j)=0である。
なお、Σ(i=1~n)r(i,j)=0は、r(i,j)=-r(j,I)から、自動的に成立する。
ただし、すべての要素がゼロとなる場合は、常にあいこであり、ゲームとして、成り立たないので、除いて考える」
「すると、三すくみで、考えるんだけど、それぞれの丸印が対等と言うことなので、各iに関する、あいこの数をa、優及び劣の数をbとすると、
Σ(j=2~n)r(i,j)=a+2b、ただし、b>=1、また、a+2b=n-1。
ここで、aには、自分自身とのあいこは含めていない。
たとえば、三すくみの場合は、n=3から、a+2b=2となるが、b>=1なので、a=0、かつ、b=1しかないことになるわね。
さっきの、r行列は、図で表すと、下図のようになる。
必ずしもゼロではない要素をx,y,zで表している。
Σ(j=1~n)r(i,j)=0から、x,y,zの間には、z=x、y=-x の関係があることが分かる。
従って、r行列は、
のようになる。
行の和がゼロという条件からは、ここまでしか分からないけど、
先ほどの条件、a(自分自身を除いたあいこの数)=0、かつ、b(優又は劣の数)=1を当てはめると、xは、ゼロにすることは出来なくなり、x=+1または-1であることが分かるわ。
すると、下図のように、2とおりの関係を表す行列が得られる」
「確かにな。
では、四すくみで考えると、三すくみのx,y,zに、u,v,wを加えて、6個となる。
煩雑のため、途中の計算を略すると、
のように、求められるな。
先ほどの条件として、a+2b=n-1=3 があるので、a=1、かつ、b=1のみが許されることになる。
そのため、
u+v=0のときは、(w-u=1、かつ、-v-w=-1)または(w-u=-1、かつ、-v-w=1)
w-u=0のときは、(u+v=1、かつ、-v-w=-1)または(u+v=-1、かつ、-v-w=1)
-v-w=0のときは、(u+v=1、かつ、w-u=-1)または(u+v=-1、かつ、w-u=1)
以上の、6とおりの場合があることになる。
第1の場合を具体的に解くと、u-w=-1、かつ、v+w=1 となるので、u=-1、v=1、w=0と決定される。
第2の場合は、u-w=1、かつ、v+w=-1 となるので、u=1、v=-1、w=0と決定される。
第3の場合は、u-w=0、かつ、v+w=1 となるので、u=1、v=0、w=1と決定される。
第4の場合は、u-w=0、かつ、v+w=-1 となるので、u=-1、v=0、w=-1と決定される。
第5の場合は、u-w=1、かつ、v+w=0 となるので、u=0、v=1、w=-1と決定される。
第6の場合は、u-w=-1、かつ、v+w=0 となるので、u=0、v=-1、w=1と決定される。
以上をまとめると、ともちゃんが言ったように、四すくみの場合の異なる配置(回転したときに重なるものは同一視する)は、6通りということになる」
「図で説明すると分かりやすいかも。
四すくみの基本形は、図Aよね。
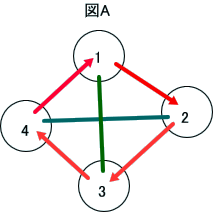
ここで、赤線は、優・劣関係を、緑線は、あいこの関係を示ししている。
1番の丸を固定して考えるとすると、2から4番までの丸の位置に2から4までを並べる数は、3!であるので、6とおりとなる。
この際、矢の向きが反対のものは、どうなるかというと、2と4との入れ替えで数えられている。
また、下図のBのような配置は、図Aの基本形と異なるように感じられると思うけど、
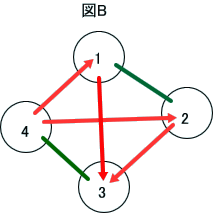
図Aで、2番と3番を入れ替えると、
次の図Cであり、
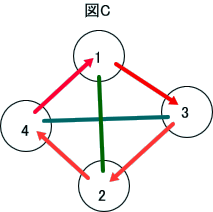
この図を変形すると、実は、図Bと同一となることが分かるので、図Bは、先の6とおりの中に含まれることが分かる」
目次に戻る
以下、分量が多いため、お急ぎの方は、次にジャンプして下さい。
「では、五すくみの場合を取り上げてみよう。
まずは、独立な要素は、n(n-1)/2で、n=5の場合の10個所となる。
一方、a+2b=4となるため、ケースを分けると、
ケース1では、a=0、かつ、b=2
ケース2では、a=2、かつ、b=1
が考えられる。
まずは、自分以外との間のあいこがない『ケース1』を考える。
ケース1では、優劣関係(+1と-1)が2組ある。
r行列の1行目の要素は、ゼロをのぞくと、4つとなるが、+1と-1の2組を選ぶ方法は、4C2=6とおりの異なったものがある。
1行目の2番目の要素の6とおりの方法は、[1,1,-1,-1]、[1,-1,1,-1],[-1,1,-1,1],[1,-1,-1,1],[-1,1,1,-1],[-1,-1,1,1]
このなかの1番目の方法では、q - s = 1 - w、 r + s = v + w、 u = -1 が得られる。
これを代入して整理すると、
2行目を見ると、1列目の要素が、-1であるため、(v,w)として、(1,1)、(1,-1)、(-1,1)の3とおりがあり得る。
(1,1)のときは、
が得られるが、sとしては、1以外は、選択できない。
これにより、
が最初の例となる。
(1,-1)のときは、s=-1となり、
(-1,1)のときは、
となって、s=+1またはs=-1の2とおりがある。
以上、4とおりの結果が得られる」
 「じゃ、私は、1行目の要素が、[1,-1,1,-1]の場合をやってみるよ。
「じゃ、私は、1行目の要素が、[1,-1,1,-1]の場合をやってみるよ。
同様に整理すると、
やはり、(v,w)として、(1,1)、(1,-1)、(-1,1)の3とおりがあり得る。
(1,1)では、s=1として、
(1,-1)では、s=1または-1として
(-1,1)では、s=1として、
となって、やはり、4とおりの組合せが得られる」
「となると、1行目の6とおりの並べ方に対して、それぞれ、4とおりの場合がありそうなので、ケース1については、6×4=24とおりではないかと予想できるのう」
「四すくみの場合と同様に考えてみたよ。
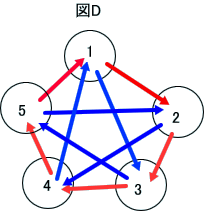
『ケース1』の場合の基本形は、図Dとなる。
1番を固定して考えると、2から5までの並べ替えで、すべての場合がつくされるので、4!=24とおりとなるのは正しいと思う」
目次に戻る
「では、『ケース2』について、取り上げてみよう。
ケース2では、(自分自身とのあいこを含めない)あいこが2、優劣の矢印が1組である。
ケース2では、1行目2列以降の要素にゼロが2個所、残りは、1と-1の組になる。
やはり、ゼロの選び方は、6とおり。しかし、残りの2個所で、+1と-1の選択が2とおりあるので、12とおりの場合に分かれる。
(1)[0,0,1,-1]として、計算してみよう。
途中で、
が得られる。
ケース1とは異なり、(v,w)の組合せとして、(1,-1)、(-1,1)、(0,1)、(1,0)、(0,-1)、(-1,0)があり得る。
(1,-1)では、s=0として、解1。
(-1,0)では、s=0として、解2。
(-1,1)、(0,1)、(1,0)、(0,-1)では、適切な解がない。
ということで、2とおりがある。
すると、ケース2では、6×2×2=24とおりがあり得るのではないかな」
 「ケース2の基本形は、図Eとなる。
「ケース2の基本形は、図Eとなる。
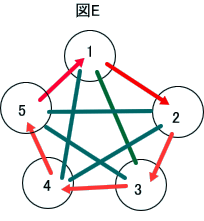
しかし、下図のFのようなものは、図Eの数字の入れ替えでは、満たせないように見える。
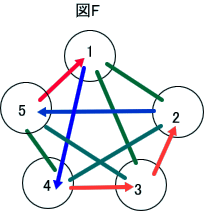
しかし、図Fで、2番と4番とを入れ替えると、図Fとなり、図Eに帰着することが分かる。
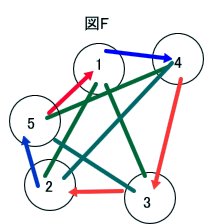
となると、ケース2についても、4!=24とおりの可能性が高いのではないかしら?」
「なるほど。
では、確かめてみよう。
(2)[0,0,-1,1]については、
中間で、次の行列が得られる。
(v,w)の組合せとして、(1,-1)、(-1,1)、(0,1)、(1,0)、(0,-1)、(-1,0)があり得る。
(1,0)について、s=0で、解3。
(-1,1)については、s=0として、解4が得られる。
その他に対しては、適切な解が得られない。
(3)[0,1,-1,0]の場合。
(0,1)として、s=0の場合に、解5。
(-1,0)として、s=-1の場合に、解6。
その他の場合は、適切な解がない。
(4)[0,-1,1,0]の場合。
(0,-1)として、s=0で、解7。
(1,0)として、s=1で、解8。
その他の場合は、適切な解がない。
(5)[1,-1,0,0]の場合。
この場合は、(v,w)として、(1,0)、(0,1)、(0,0)が許される。
(v,w)として、(0,1)とすると、s=1として、解9。
(v,w)として、(0,0)とすると、s=-1として、解10。
その他の場合は、適切な解がない。
(6)[-1,1,0,0]の場合。
この場合は、(v,w)として、(0,-1)、(-1,0)、(0,0)が許される。
(0,-1)として、s=-1とすれば、解11。
(0,0)として、s=1とすれば、解12。
その他の場合は、適切な解がない。
(7)[1,0-1,0]の場合
(v,w)として、(0,1)、(1,0)、(0,0)が許される。
(1,0)として、s=-1とすれば、解13。
(0,0)のときは、s=0で、解14が得られる。
その他の場合は、適切な解がない。
(8)[-1,0,1,0]の場合
(v,w)として、(0,0)、(-1,0)、(0,-1)があり得る。
(0,0)の場合は、s=0として、解15。
(-1,0)の場合は、s=1として、解16。
その他の場合は、適切な解がない。
(9)[0,1,0,-1]の場合
(v,w)として、(1,-1)、(-1,1)、(0,1)、(0,-1)、(-1,0)、(1,0)があり得る。
(0,-1)として、s=0で、解17。
(-1,1)では、s=1として、解18。
その他の場合は、適切な解がない。
(10)[0,-1,0,1]の場合
(v,w)として、(1,-1)、(-1,1)、(0,1)、(0,-1)、(-1,0)、(1,0)があり得る。
(1,-1)では、s=0で解19。
(0,1)では、s=0として、解20。
その他の場合は、適切な解がない。
(11)[1,0,0,-1]の場合
(v,w)として、(1,0)、(0,1)、(0,0)があり得る。
(1,0)では、s=1として解21。
(0,1)では、s=1として、解22。
その他の場合は、適切な解がない。
(12)[-1,0,0,1]の場合
(v,w)として、(-1,0)、(0,-1)、(0,0)があり得る。
(-1,0)では、s=-1として、解23。
(0,-1)では、s=0で、解24。
その他の場合は、適切な解がない。
となり、ケース2では、24とおりであるな」
「やっぱり!」
「ということは、n=5の五すくみでは、回転して、同一となるものを同じと見なすと、ケース1とケース2を合わせて、48とおりであることが分かる」
目次に戻る
「前節までの例から、一般の場合を予想してみよう」
 「そうね。
「そうね。
Nすくみの場合は、N とあいこの組数(M)で特徴付けられるので、一般には、M×(N-1)!通りじゃないかと思う」
「では、表にしてみると、次のようじゃな。
ただし、あいこの数には、自分自身へのあいこも含めてある。
六すくみ以上では、手計算で確認することが困難なので、コンピュータで確認してみよう」
「それがね。
不思議なんだけど。
N=3~5までは、予想のM×(N-1)!と等しかったけど、N=6では、240ではなくて、シミュレーションでは、730になるんだな、コイツが。
簡単に言うと、六すくみの場合は、あいこの数が2の場合が、570個、あいこの数が4の場合が、160個の合計730個ということになるの」
「七すくみでは、どうじゃったのかな」
「六すくみでは、52秒程度の時間で求まったのだけど、七すくみでは、12時間近くかかってしまったわ。
結果は、あいこの数が1の場合は、2,640個、3個の場合が27,900個、5個の場合が1,140個の合計31,680個という結果に・・」
| すくみの数(N) | あいこの数 | あいこの組数(M) | 可能なゲームの組合せ数(予想) | 組合せ数(シミュレーション) | 予想(その2)(2013/1/14) | 備考 |
| 3 | 1 | 1 | 2 | 2 | 1.99 | 三すくみ(1×2!) 普通のじゃんけんも一例 |
| 4 | 2 | 1 | 6 | 6 | 6.18 | 四すくみ(1×3!) |
| 5 | 1,3 | 2 | 48 | 48 | 45.1 | 五すくみ(2×4!) |
| 6 | 2,4 | 2 | 240 ? | 570+160=730 | 773 | 六すくみ 球磨拳も一例 |
| 7 | 1,3,5 | 3 | 2,160 ? | 2,640+2,7900+1,140=31,680 | 31,200 | 七すくみ |
| 8 | 2,4,6 | 3 | 15,120 ? | ? | 3×10^6 ? | 八すくみ |
| 9 | 1,3,5,7 | 4 | 161,280 ? | ? | 6×10^8 ? | 九すくみ |
| 10 | 2,4,6,8 | 4 | 1,451,520 ? | ? | 3×10^11 ? | 十すくみ |
| 11 | 1,3,5,7,9 | 5 | 18,144,000 ? | ? | 4×10^14 ? | 十一すくみ |
| 12 | 2,4,6,8,10 | 5 | 199,584,000 ? | ? | 1×10^18 ? | 十二すくみ 干支拳も一例 |
「なるほど。
ともちゃんのプログラムの『総当たり方式』では、だいたい、3^(N(N-1)/2)に比例する時間がかかる。
この、N(N-1)/2は、上三角行列の要素の個数じゃ。3のべきとなっているのは、+1、-1、0の3つの状態があるからじゃな。
よって、N=6の場合が52秒だとしても、N=7では、約730倍の時間、すなわち、11時間弱が必要になったというわけじゃ。
ところで、ExcelのVBAで、ともちゃんが書いてくれたプログラムのアルゴリズムの再検討も含めて、この問題については、後日、あらためて考えることにしようかの。
いや。年末から、ともちゃんも、お疲れさんじゃったな」
「一応、N=3~6までの結果を下に記しておくよ。
N=3~6の場合。
なお、七すくみの場合は、結果が膨大なので、今回は、リンクを張っていません。
下図が、n=3の場合。
ここで、白丸は、+1を、黒丸は、-1を、そして、×は、ゼロを表すことにしたわ。
次の、PDFファイルは、n=4の場合。
sukumi4.pdf
また、次のPDFファイルは、n=5の場合よ。
sukumi5.pdf
そして、下が、問題のn=6の場合ね。(100ページ以上あります)
sukumi6.pdf
確認用に、エクセル表も添付してあります。(下図は、最初の部分)
このエクセル表のBangoは、sukumi6.pdfの番号と同一。
また、zeroは、自分自身へのあいこの数を含み、ITIは、+1の個数とする。
MOJIは、対角線上と右上三角行列部分の記号文字列です。
sukumi6excel.xlsx
2013/1/14の追記の際にエクセル表を差し替えました。MOJIの隣にKEIROの列を追加して、点1からすべての点を巡回出来る場合は、その順路を記載しました。
出来ない場合は、『全点を巡回は不能』と表示しました」
※今回の問題は、見方によっては、一般に『魔方陣』と呼ばれるものの『退化』した例であると思われます。
通常の魔方陣は、n×nのマス目(n>=3の整数)に1~n^2の相異なる正数を配置して、縦、横、斜めの各合計(『定和』と呼ばれる)が一定であるようにしたものです。
上で、『退化』と書いた意味は、すくみの問題では、定和は、ゼロで一定であり、その意味では、魔方陣と同様なのですが、同一の数字が何カ所にも現れています。
すなわち、数字の種類を、ゼロ、+1、-1の3種類に限っているためです。また、±1の個数にも、すくみの関係から来るところの制限があります。
たとえば、n=3の例で出てきた、左上図の関係行列の各要素に対して、ゼロ→d、+1→d+f、-1→d-fという変換を施すと、左中図のようになります。
ここで、d及びfに任意の数値、ここでは、d=5、f=2、を代入すると、左下図のように魔方陣の『退化』した例となります。
また、付言すれば、魔方陣は、それ自体、物理的な意味が希薄(魔方陣に類似した『ラテン方陣』のように実験計画法に使用されるものもありますが)であるのに対して、『すくみ』の問題の場合は、ゲームルールに直接、関係がある点で、興味深いものがあります。
なお、魔方陣の場合は、コンピュータを使用しても、n=5程度までしか、すべての解を求めることができません。これは、可能な解の探索範囲が極めて広くなるからです。
一方、今回の問題では、文字数の制限等から、探索範囲が狭くなり、結果として、n=7程度まで、すべての解を求めることができました。
(本節の青字部分は、2013/1/8 追記しました。ただし、『予想その2』は、2013/1/14に追加しました。)
目次に戻る
「ようやく、胸のつかえが取れましたな」
 「ご隠居様、お餅を召し上がり過ぎではございませんか」
「ご隠居様、お餅を召し上がり過ぎではございませんか」
「これは。お銀さん。恥ずかしいのう」
「ちょっと、ちょっと、何をやらせるんですか!」
「おっと、すまんのう。
どうしても、納得いかんもんじゃったのでな。
ほれ、年末に『六すくみ』の場合、『あいこの数が4の場合が、160個』と書いた」
「ええ、コンピュータのシミュレーションでは、160個だったですから」
「ところが、予想では、この場合はどうしても、5!=120とおりと、考えられるではないかのう」
「変なのよね~」
「そこで、お正月休みの間に、ひそかに調べましたぞ。
と、こういうわけなのじゃ」
「なるほど」
「まだ、何も言っておらんじゃろうが・・。
つまりじゃ、六すくみの中に、三すくみ+三すくみが混じっていたのじゃ。
これまで、考えていた、六すくみの中の、あいこの数が4つの場合は、下の図Aの場合だった。
(矢印は、勝ち負けを表し、矢羽根のない線分は、あいこの関係を表す)
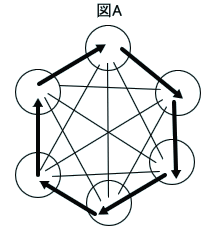
ところが、シミュレーションの160個の中には、図Aに加えて、下図のBのようなものも混ざっていたのじゃ。
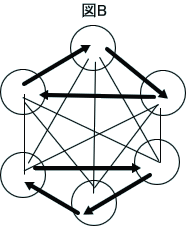
これでも、あいこの数が4つ(自分自身へも含めて)で、勝ち、負けの数は平等じゃ」
「う~ん。図Bは、六すくみとしては、反則気味だけど。
とは言え、図Aの場合が、予想のように、5!=120とおりで、図Bはというと、6個のうちから3つをとる場合の20とおりの2倍で、40とおり。
ここで、2倍しているのは、三すくみの場合の異なる組の数が2だからだけど、この数の和が、120+40=160ということね」
「そういうことじゃな。
確かに、図Bを『六すくみ』というのは抵抗があるのは事実じゃがな。
とは言え、コンピュータに与えた条件を満たしているのも本当じゃ。
要は、『すくみ』の定義次第ではあるが、予想とシミュレーションの食い違う訳が分かったことになるのではないかな。
五すくみまでは、このような、『組』(サブネット)ができないので、予想とシミュレーションの結果とが一致したのじゃろう。
今のところ、詳しく検討しきれていないが、あいこの数が2の場合の、570とおりというのも、このような、複数の『組』の存在で説明できるのではないかと思う」
「なるほど、ガッテンです。
予想もまんざら外れてはいなかったのね」
「しかし、負うた子ならぬ、使ったコンピュータに教えられた、とも言えるの。
ま、お正月じゃから、『あいこ』と言うことで、どうじゃろうかな」
「勘弁してあげましょう」
※『六すくみ』のあいこの数が24の場合で、上記の三すくみ+三すくみの40個については、点1を出発して2~6までのすべての頂点を関係行列の値が+1のもののみを経由してたどるルートがあるかどうかを確認する手段を使うと、区別できることが分かりました。
なお、出発点は、点1でなくても同等です。また、関係行列の値が+1である点をたどるのではなく、-1である点をたどるとしても同等です。
(すべての点をたどる経路(必ずしも最短経路でなくてもよい)を調べるのは、nが小さいときは、単純な再帰手続きを使うことにより容易なのですが、再帰手続き自身の構成について、いつものことながら、悩んでしまいました・・)
しかし、『六すくみ』のあいこの数が42つの場合の570個については、この手段では、相互に区別できないことも分かりました。
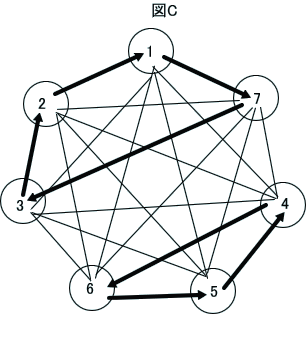
また、『七すくみ』の場合は、あいこの数が5の場合の1,140個のうち、420個は、六すくみと同様に「サブグループ」(三すくみ+四すくみ)に分かれており、点1を出発して2~7までのすべての頂点を経由する経路がないことも分かりました。
この420個は、7つのうちから4つを選ぶ方法=35に四すくみの場合の6とおりをかけて、210個、この数値に、更に、三すくみの2とおりをかけて得られる420個であると考えられます。
(下図C)
しかし、その他のあいこの数の場合には、やはり、これだけでは、分類することが出来ませんでした。
私見では、このような問題は、数学の『グラフ』(有向グラフ)理論を使って、より、適切な分類、分析が可能であると思われます。
今回は、グラフ理論等に関する当方の知識不足のために、関係行列を基にした分析をこれ以上進めることが出来ませんでしたが、今後、機会があれば、振り返ってみたいと思います。
なお、n=3~7までのシミュレーションの結果から、n=8以降の組合せ数を外挿して予想し前節の表に『予想その2』として追加しました。
まあ、もとより、不確実な数値ではありますが、組合せ数というものの『爆発的威力』を実感します。
(本節の青字部分は、2013/1/13、1/14に追記しました)
※本節の赤字の部分にミスがありましたので、取り消し線にて消去し、正しい数に訂正しました。(2015/11/25)
目次に戻る
干支拳は、いわゆる、手を使う『じゃんけん』で行うのは、無理でしょう。
そこで、干支拳カードなるものを作ってみました。A4サイズのやや厚手の紙(裏に透けないもの)に印刷すると良いでしょう。
2ページ分で1組(黒と赤)です。
裏の模様もアップしてあります。裏を印刷する必要はありませんが、真っ白のままよりも、トランプっぽい雰囲気があるとは思います。
PDF形式:干支拳カード(etokencard.pdf)
同じく、: 干支件カードの裏の模様(etokenura.pdf)

目次に戻る
今回もご覧いただき、ありがとうございました。
また、来月も、本欄で元気にお会いできますことを願っています。
目次に戻る