数式処理ソフト DERIVE(デライブ) de ドライブ
60.楕円積分と楕円関数(1)
第1種楕円積分とヤコビの楕円関数
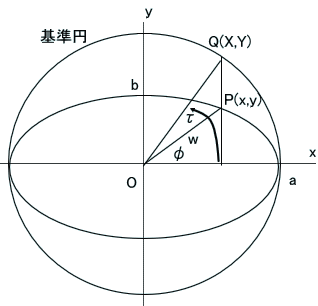
数式処理ソフト DERIVE(デライブ)の第59回『数値積分(外伝:√t×sin(t)のラプラス変換とベッセル関数)』でともちゃんに計算してもらった、楕円上の点P(x,y)と楕円の中心との距離を表す wは、w=a√(1-ε^2)/√(1-(εcos(φ))^2)であった。ここで、x軸からP点へ反時計回りにφを計っている。
 さて、wは、ヤコビの楕円関数で表すことができることが分かったので、それに関して、記載する。
さて、wは、ヤコビの楕円関数で表すことができることが分かったので、それに関して、記載する。
なお、ここでは、『楕円関数入門』(戸田盛和著:日本評論社:2001年9月)などを参考にしているが、一部、DERIVEの表記に合わせて、記号等を変更している。
なお、筆者は、楕円積分及び楕円関数について、にわか勉強のため、不適当な記述又は誤りがあるかもしれないことを、予め、お断りしておきます。
最初に、sn(u,k)(エスエヌ関数)について、定義する。
まず、u(x)=∫(0-x)1/√((1-t^2)(1-k^2t^2))dt、ここで、積分範囲 xは、-1=<x<=1で考える。
また、k を母数(modulus)といい、範囲は、k=0~1とする。
u(x)の逆関数を、x=sn(u)と書いて、ヤコビのsn(u,k)(エスエヌ)関数という。
kは、母数に依存していることを明らかにするために記す。
なお、「ヤコビの」と断っているのは、楕円関数の表記について、ルジャンドル-ヤコビの表記法以外にいくつかの表記の仕方があるためである。
しかし、これでは、あまりに天下り式であるし、「逆関数」の概念自体がわかりにくいので、もう少し、説明を加える。
今、y=f(x)という関数があるとき、この式をxに関する方程式とみて、xについて、解いた(つもりの)式、x=g(y)のg(y)をf(x)の逆関数という。
たとえば、y=f(x)=2x+1のときに、x=(y-1)/2、g(y)=(y-1)/2をf(x)の逆関数と言う。
普通、ここで、g(y)の()内の変数名yをxに変えて、g(x)と書くが、ここでは、わかりにくくなるので、しばらくyのままにしておく。
さて、上のf(x)とg(y)は、関数と逆関数が一対一に対応しているが、f(x)=x^2のような関数でも、逆関数である、√yは、正負、2つの種類ができる。
また、三角関数とその逆三角関数についても、同様に、たとえば、sin(x)とAsin(y)のように、逆関数である、Asin(y)は、(無限)多価関数となる。
すなわち、たとえば、Asin(1/2)の値は、π/3、(sin(π/3)=1/2)であるが、sin(π/3±2nπ)も、また、同じ値1/2を返す。このようなときは、-π/2~π/2の範囲の値をAsin(y)の「主値」といって、その範囲内では、一価となるようにしている。
指数関数と逆関数である対数関数も、対数関数が多価になる。このように逆関数が多価となる場合が特にわかりにくい。
下図は、k=0、0.8、1の場合の、u(x)のグラフである。横軸は、x、縦軸は、u(x)。
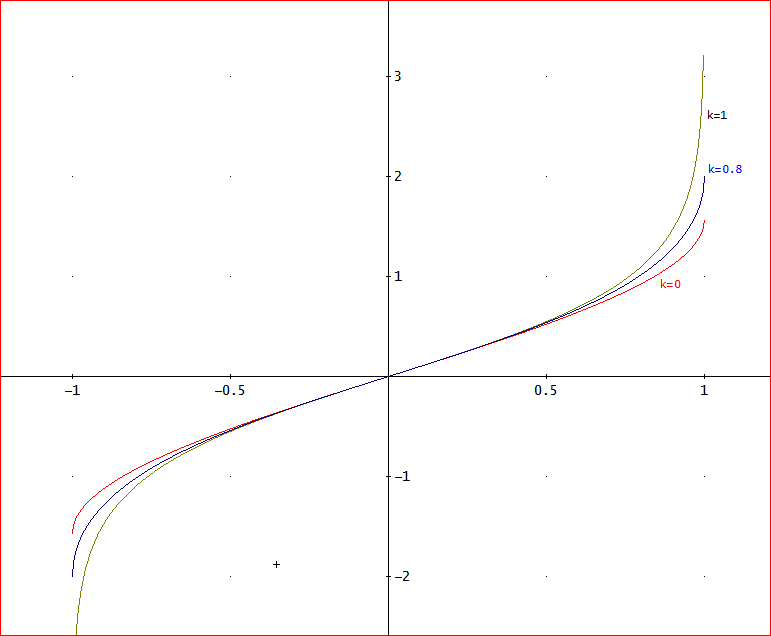
ところで、
∫(0-x)1/√((1-t^2)(1-k^2t^2))dtにおいて、t=sin(θ)と置き、F(φ,k)=∫(0-φ)1/√(1-k^2sin^2(θ))dθ、と書き直してみる。
ここで、φは、x=sin(φ)となる角度で、積分は、θ=0~φまで、積分することを意味する。左辺のF(φ,k)は、「第1種楕円積分」という。
なお、特にφ=π/2のとき、K(k)≡∫(0~π/2)1/√(1-k^2sin^2(θ))dθを「第1種完全楕円積分」といい、K(k)で表す習慣がある。
DERIVEでは、EllipticIntegrals.mthを開くか、読み込むかすると以下の関数が使える。
ELLIPTIC_F(φ, m)は、第1種楕円積分を表す。ただし、DERIVEでは、母数kに対して、m=k^2の関係にあるmで表しているため注意が必要である。
下表は、k=0~1まで、0.1刻みで、DERIVEで計算したK(k)及びK(k')の値である。ここで、補母数 k'=√(1-k^2)、K(k')=K'とも記する。
| k |
K(k) |
K'=K(k') |
| 0 |
π/2≒1.570796326 |
∞ |
| 0.1 |
1.574745561 |
3.695637362 |
| 0.2 |
1.586867847 |
3.016112492 |
| 0.3 |
1.608048619 |
2.627773332 |
| 0.4 |
1.639999865 |
2.359263554 |
| 0.5 |
1.685750354 |
2.156515647 |
| 0.6 |
1.750753802 |
1.995302777 |
| 0.7 |
1.845693998 |
1.862640802 |
| 0.8 |
1.995302777 |
1.750753802 |
| 0.9 |
2.280549138 |
1.654616667 |
| 1.0 |
∞ |
π/2≒1.570796326 |
なお、戸田先生の本とF(φ,k)のφとkの順序をDERIVEに合わせて、変えている。
さて、F(φ,k)の逆関数を、φ=am(F)と書き、これをヤコビの振幅関数という。
冒頭に述べたように、x=sn(u)であるが、上式からは、x=sin(φ)=sin(am(F))=sn(F)と書けることが分かる。
すなわち、sn(u,k)=sin(am(F))により、これから、エスエヌ関数を計算することができる。
kが特別の値、k=0のときは、F(φ,0)=φであり、φ=am(F)=Fから、sn(F)=sin(am(F))=sin(F)となる。
ここで、Fを通常使用する変数、uと書き換えれば、sn(u,0)=sin(u)となる。すなわち、k=0の場合は、sn関数は、sin関数と同一になる。
また、k=1のときは、F(φ,1)=LN(cos(φ)/(1-sin(φ))となり、これから、φ=am(F)=2Atan(exp(F))-π/2となる。
なお、k=1のときは、逆三角関数の多価性から、定数だけ異なる無限のケースがあるが、φ=0でF=0となる分枝を選択している。
よって、sn(F)=sin(2Atan(exp(F))-π/2)=Tanh(F)なので、sn(u,1)=Tanh(u)となる。k=1の場合は、sn関数は、双曲線タンジェント関数になる。
しかし、一般のkについては、閉じた形で振幅関数、amを与えることはできない。
近似式としては、岩波数学辞典(第4版)巻末の公式に、am(F,k)=πF/(2K)+Σ(n=1~∞)(2Q^(n)/(n(1+Q^(2n))×sin(nπF/(2K)))
ここで、K=K(k)なる第1種完全楕円積分、また、K'は、補母数k'=√(1-k^2)としたとき、K(k')をK'と略記している。
また、Qは、exp(-π(K'/K))である。
Σの第1項までとった場合、具体的な表式は、k=0~1まで、0.1刻みで次のとおり。
| k |
am(x,k) |
| |
Σの第1項まで |
| 0 |
x |
| 0.1 |
0.001256290825SIN(0.9974921442x) + 0.9974921442x |
| 0.2 |
0.005102671812SIN(0.9898721744x) + 0.9898721745x |
| 0.3 |
0.01178787934SIN(0.9768338514x) + 0.9768338514x |
| 0.4 |
0.02178813757SIN(0.9578027166x) + 0.9578027166x |
| 0.5 |
0.03593316736SIN(0.9318083916x) + 0.9318083916x |
| 0.6 |
0.05568492303SIN(0.8972114321x) + 0.8972114321x |
| 0.7 |
0.08382263740SIN(0.8510599959x) + 0.8510599959x |
| 0.8 |
0.1265104978SIN(0.7872471007x) + 0.7872471007x |
| 0.9 |
0.2025825880SIN(0.6887798646x) + 0.6887798646x |
| 1.0 |
(近似不可) |
そして、sn(x,k)=sin(am(x,k))、ここで、am関数は、Σの項数10項まで使って、k=0,0.5,0.8でグラフにしたものを
下図に示す。
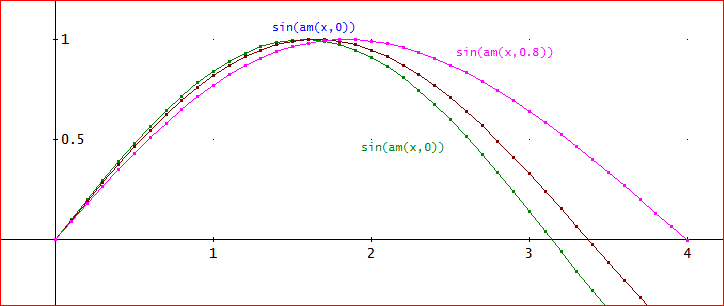
各、sn(x,k)がx軸と交差するxは、sn関数の0の次の最初のゼロ点であり、2K(k)で表される。
2K(0)=π≒3.141592653
2K(0.5)≒3.371500709
2K(0.8)≒3.990605555
これを見ると、グラフとの一致は、まずまずである。
なお、k=1については、前述のように周期関数にならずに、sn(x,1)=Tanh(x)のようにx→∞で1に収束する単調増大関数となるので、上記近似式では、近似できない。
※k=1のときのam(F)=2Atan(exp(F))-π/2となるが、これは、am(F)≡gd(F)として、Gudermann(グーデルマン)関数と言われる。
※DERIVEでは、am関数は、EIF(φ, m, n)として、近似的に定義されている。この中で、m=k^2、また、nは、近似度合いを表すパラメータ(1~)である。
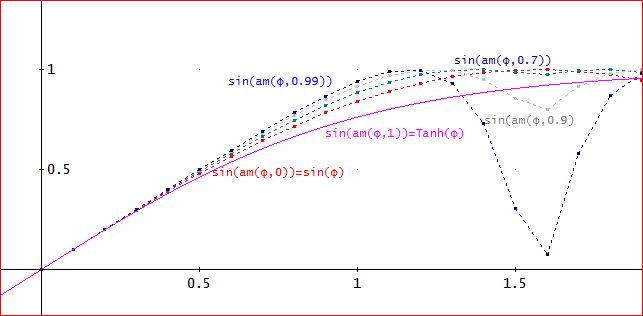
ただし、kが大きいときは、φがπ/2+2nπ(n=0、±1・・)付近に、近似誤差と思われる見かけ上の「谷」が現れている。
前述の岩波数学辞典付録の公式による方が近似誤差が少ないようであるが、詳細は、不明。
さて、sn(u,k)関数は、これまでのところ、u=-K(k)~K(k)の間で定義されているが、これをつないで、周期4K(k)の関数を作る。これをuが実数域でのsn(u,k)関数とする。
また、cn(u,k)=√(1-sn^2)として、cn(u,k)という、シーエヌ関数を定義する。定義からも分かるように、cn関数は、cos(x)(コサイン関数)に似ている。
定義とam関数から、cn^2=1-sn^2=1-sin^2(am(F))=cos^2(am(F))となるので、cn関数は、cn(u,k)=cos(am(u,k))とam関数を通じて計算可能である。
母数、kが特別の値の場合は、cn(u,0)=cos(u)、cn(u,1)=sech(u)=1/cosh(u)となる。
sn関数と同様に、適宜、つないで、周期4K(k)の関数を作り、これをcn(u,k)関数とする。
下図は、cn(x,k)=cos(am(x,k))、ただし、Σの項数は、10項まで、k=0、0.5、0.8のグラフ。
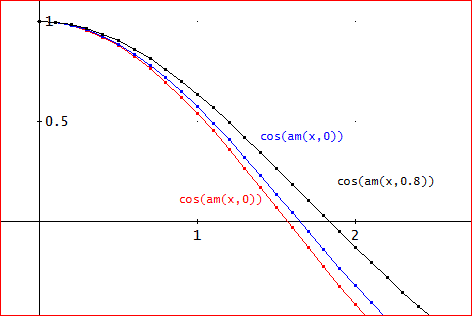
定義から明らかであるが、cn関数の正の最初のゼロ点は、K(k)である。
ちなみに、グラフで描いたkについては、次のとおり。
K(0)=π/2≒1.57079632
K(0.5)≒1.685750354
K(0.8)≒1.995302777
近似は、傾向としては、問題はないようである。
更に、dn(u,k)、ディーエヌ関数を√(1-k^2sn^2(u,k)) で定義する。dn関数は、周期2K(k)となる。
特別な値、dn(u,0)=1、dn(u,1)=cn(u,1)=sech(u)となる。
第2種楕円積分と第3種楕円積分
第1種楕円積分に似た形の∫(0-φ)√(1-k^2sin^2(θ))dθは、第2種楕円積分と呼ばれ、E(φ,k)で表される。
DERIVEでは、ELLIPTIC_E(φ, m)で表される。F(φ,m)と同様にm=k^2なので注意が必要である。
φ=π/2のときの値、F(π/2,k)を第2種完全楕円積分と呼び、E(k)で表す。
同様に第3種楕円積分、π(φ,k,n)=∫(0-θ)1/((1+n sin^2(θ))(√(1-k^2sin^2(θ)))dθ、ここで、nは、パラメータと呼ばれる。
DERIVEでは、ELLIPTIC_PI(φ, m, n)と書かれている。m=k^2、n=-nなので、特に注意が必要である。
第1種楕円積分の場合と同様に、E(θ,k)とπ(θ,k,n)も戸田先生の本に比して、変数φと母数 k、パラメータ nの順序を変えて記載している。
一般に、√(xの1次式)、√(xの2次式)、1/√(xの1次式)、1/√(xの2次式)は、初等関数で不定積分が求まる。
同様に、√(xの3次式)、√(xの4次式)、1/√(xの3次式)、1/√(xの4次式)は、楕円積分の第1種から第3種のいずれかの標準形に積分変数の変換で変形可能である。
変換式は、たとえば、岩波数学辞典(第4版)付録の公式集に掲載されているので、ここでは、割愛する。
また、根号内の整式によっては、楕円積分ではなく、初等関数で表される場合もある。それらを「擬楕円積分」ともいう。
楕円関数の微分
まず、sn関数の微分を考える。
sn(F,k)=sin(am(F,k))なので、両辺をFで微分すると、d/dF(sn(F,k))=cos(am(F))×d(am(F)/dF)=cn(F,k)×dF/d(am)となる。
ここで、F(φ,k)=(0-φ)1/√(1-k^2sin^2(θ))dθから、dF/dφ=√(1-k^2sin^2(φ))、
また、φ=am(F)であるので、d/d(am)=d/dφとなるので、dF/d(am)=dF/dφ=√(1-k^2sin^2(φ))=√(-k^2sin^2(am(F))=√(-k^2sn^2(am(F))
dn関数の定義から、√(-k^2sn^2(am(F))=dn(F,k)、
よって、d/dF(sn(F,k))=cn(F,k)×dn(F,k) となる。通常使う変数名に戻せば、sn'(u,k)=cn(u,k) dn(u,k)である。
同様に、cn(F,k)=cos(am(F))なので、両辺をFで微分すると、d/dF(cn(F))=-sin(am(F))×d(am(F)/dF)=-sn(F,k)×dF/d(am)となる。
上と同様に、dF/d(am)=dn(F,k)を使うと、d/dF(cn(F))=-sn(F)×dn(F) となるので、通常使う変数名に戻せば、cn'(u,k)=-sn(u,k) dn(u,k)である。
また、dn^2(F)=1-k^2 sn^2(F)から、両辺をFで微分すると、2 dn dn'=-2 k^2 sn cn dn なので、dn'(F)=-k^2
sn(F)cn(F)より、
通常使う変数名に戻せば、dn'(u,k)=-k^2sn(u,k) cn(u,k)である。
楕円積分の楕円関数による表示
第1種楕円積分は、F(φ,k)=∫(0-φ)1/√(1-k^2sin^2(θ))dθであるが、θをam(F)と変換すれば、
被積分関数は、1/√(1-k^2sin^2(am(F))×d(am)/dF=1/dn(F)×d(am)/dF、となる。
ここで、dF/d(am)=dn(F)であるので、
F(φ,k)=∫(0-F0)(1/dn(F)×dn(F) dF=F0、
しかし、φ=am(F0)なので、逆関数を考え、amの逆関数がF(φ,k)であることを思い出すとF0=F(φ,k)。
結局、F(φ,k)⇔sn(F,k)の関数と逆関数との関係を再確認することとなる。
次に、第2種楕円積分を楕円関数の積分で表すことを考える。
第2種楕円積分は、E(φ,k)=∫(0-φ)√(1-k^2sin^2(θ))dθであるが、θをam(F)と変換すれば、
sin(θ)=sin(am(F))=sn(F)、dθ=d(am)=d(am)/dF dF=dn(F) dFから、
被積分関数は、√(1-k^2sin^2(θ))=√(1-k^2sn^2(F))×dn=dn×dnとなる。
従って、E(φ,k)=∫(0-F0)(dn^2(F,k)) dF≡ε(F0)、ここで、φ=am(F0)から、F0=F(φ,k)である。
この、∫(0-u)(dn^2(u,k) du)は、ヤコビのエプシロン関数ともいい、ε(u)で表される。(ここは、通常使われる変数uを使って書いた)
第3種楕円積分、π(φ,k,n)=∫(0-θ)1/((1+n sin^2(θ))(√(1-k^2sin^2(θ)))dθは、同様に、θをam(F)と変換すれば、
被積分関数は、1/((1+n sn^2)(√(1-k^2sn^2))×dn=1/(1+n sn^2)となるので、
π(φ,k,n)=∫(0-F0)(1/(1+n sn^2)dFと書くことができる。ここで、φ=am(F0)から、F0=F(φ,k)である。
ただし、以上は、理論的なことであり、数値計算上からは、楕円関数に変換して楕円積分を計算する利点は、少ないと思われる。
楕円関数の加法定理
楕円関数の微分は、三角関数に比して、やや、複雑であるが、楕円関数の加法定理(公式)は、比較にならないくらいの複雑さとなる。
証明なしに掲げる以下の基本的な公式がある。
sn(u+v)=(sn(u) cn(v) dn(v) + sn(v) cn(u) dn(u))/(1-k^2 sn^2(u) sn^2(v))
cn(u+v)=(cn(u) cn(v) -sn(u) sn(v) dn(u) dn(v))/(1-k^2 sn^2(u) sn^2(v))
dn(u+v)=(dn(u) dn(v) -k^2 sn(u) sn(v) cn(u) cn(v))/(1-k^2 sn^2(u) sn^2(v))
これは、別の書き方では、
sn(u+v)=(sn^2(u)-sn^2(v))/(sn(u) cn(v) dn(v) - sn(v) cn(u) dn(u))
cn(u+v)=(sn(u) cn(u) dn(v) - sn(v) cn(v) dn(u))/(sn(u) cn(v) dn(v) -sn(v)
cn(u) dn(u))
これに加えて、次の式も有用とのこと。(トムソン(J. J. Thomson)の式)
(dn(u) cn(v) - cn(u) dn(v))/(sn(u)-sn(v))=(dn(u+v)-cn(u+v))/sn(u+v)
楕円関数とwとの関係
以上、長々と、楕円関数について、入門的な記事を書いてきた。
ここで、原点を中心とする楕円のいくつかの計量を楕円関数等で表すことを試みる。
楕円の標準形、(x/a)^2+(y/b)^2=1を出発点とする。また、離心率、ε=√(1-(b/a)^2)である。
まずは、楕円上の点P(x,y)を楕円関数で表す。
以下では、第1象限を考える。
a^2y^2=a^2b^2-b^2x^2 より、離心率εを使うと、
y^2=a^2(1-ε^2)-(1-ε^2)x^2=(1-ε^2)(a^2-x^2)である。
ψ=π/2-φなる、角度 ψを使うと、x=w*cos(φ)=w*sin(ψ)より、
y^2=(1-ε^2)(a^2-w^2sin^2(ψ))
ここで、ψ=am(F)と置いてみると、
y^2=(1-ε^2)(a^2-w^2sin^2(am(F))=(1-ε^2)(a^2-w^2sn^2(F))と書ける。
よって、w^2=x^2+y^2に代入すると、w^2=w^2sin^2(ψ)+(1-ε^2)(a^2-w^2sn^2(F))から、
w^2=w^2sn^2+(1-ε^2)(a^2-w^2sn^2)=(1-ε^2)a^2+ε^2w^2sn^2 になり、移項すると、
w^2(1-ε^2sn^2)=a^2(1-ε^2)なので、もし、k≡εであれば、w^2(1-k^2sn^2)=a^2(1-k^2)
ここで、dn(F,k)=√(1-k^2sn^2(F,k))を使うと、w=a√(1-k^2)/dn(F,k)、ここで、F=F(ψ,k)、右辺は、第1種楕円積分である。
この表示は、前回の記事の、w=a√(1-ε^2)/√(1-(εcos(φ))^2) からも、直接、求められる。
一方、ψ=am(F)だったので、sin(ψ)=sn(F,k)、dn(F,k)=√(1-k^2sn^2(F,k))=√(1-k^2sin^2(ψ))を使えば、
w=a√(1-k^2)/dn(F,k)=a√(1-k^2)/√(1-k^2sin^2(ψ))と元の表式に戻る。
これから、楕円上の点の位置は、中心との距離 wとy軸からの角度ψを使って、下のように求められる。
x=w*sin(ψ)=a√(1-k^2)/dn(F,k)×sin(ψ)=a√(1-k^2)×sn(F,k)/dn(F,k)
y=w*cos(ψ)=a√(1-k^2)/dn(F,k)×cos(ψ)=a√(1-k^2)×cn(F,k)/dn(F,k)
F=F(ψ,k)=∫(0-ψ)1/√(1-k^2sin^2(θ))dθ
上記は、複雑であるが、楕円の標準形に入力して、正しいことを確認できる。
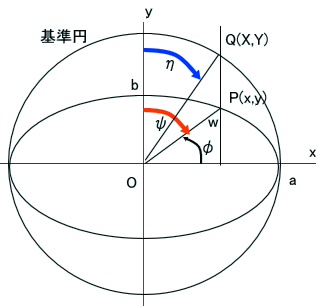
なお、通例のように、中心Oと基準円上の点Q(X,Y)を結ぶ線分へのy軸からの角度、ηを使えば、
x=a*sin(η)=a*sn(u,k)
y=b*cos(η)=b*cn(u,k)
と簡潔に書くことができるが、ηは、点PとOとを結ぶ線分の角度ではないことに注意する必要がある。
ここで、η=am(u)より、sin(η)=sn(u)などと変換している。
前者から、x/y=sn(F)/cn(F)=sin(ψ)/cos(ψ)=tan(ψ)
後者からは、x/y=(a/b)tan(η)
比較すると、tan(ψ)=(a/b)tan(η)となる。
前回に示した、Tan(φ)=(b/a)Tan(τ)=√(1-ε^2)Tan(τ)と比較すると、異なるようにも見えるが、今回の式で、
ψ=π/2-φ、η=π/2-τとおけば、tan(ψ=)tan(π/2-φ)=1/tan(φ)、また、tan(η)=1/tan(τ)より、
1/tan(φ)=(a/b)(1/tan(τ))となるので、ひっくり返すと、前回の式と同一であることが分かる。
終わりに
以上、「楕円関数」について、ざっと見て来ましたが、予想どおり、とても、一回で済ませることはできないことが明らかになりました。
機会があれば、また、続きを書いていきたいと思います。
特に、楕円積分は、DERIVEに備えられていますが、ヤコビの楕円関数は、用意されていないので、sn、cn、dn関数をもう少し、丁寧に計算してみたいと思います。
また、前回(第59回)、楕円の中心と楕円周上の点との距離wを極座標で書いた場合に正しく楕円が表示されることを狙ったところから、徐々に深みにはまった感があります。
もちろん、パラメータ τにより、[a cos(τ),b sin(τ)]のように与えれば、DERIVEの「直交座標」で楕円を表示させることは、容易なことなのです。
しかし、r=a(1-ε^2)/(1+εcos(θ))のように、与えて、極座標として扱えないか、という視点です。上記で与えている、wは、φにより、極座標で楕円を描くことができます。
ただし、今回、wを楕円関数で表してみましたが、特に気の利いた使い方ができないようにも思えます。何か、この表記が役に立つことがないかを考え中です。
※9/6にタイトルを変更しました。
最終更新日 2011/9/7



 さて、wは、ヤコビの楕円関数で表すことができることが分かったので、それに関して、記載する。
さて、wは、ヤコビの楕円関数で表すことができることが分かったので、それに関して、記載する。
