
初春驚窓辺兎組合数(はつはるのおどろきまどべのうさぎくみあわせのかず)
アッカーマンの関数
クヌースの矢印表記
2進数等との関係
x↑↑n の変化
無限大
終わりにあたって
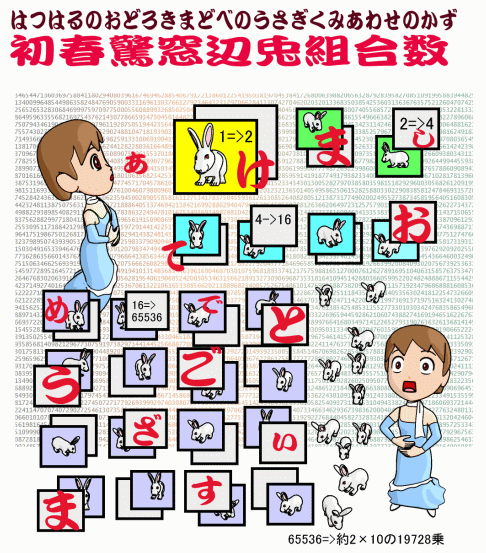
「いざ、初春を寿ぎて驚きの数をご覧にいれまする。
題して「初春驚窓辺兎組合数」(はつはるのおどろきまどべのうさぎくみあわせのかず)。
さ~て、窓1つでは、兎が見える、見えないの2通りでございます。
窓数を2つから、前の組合せに等しく増やしていけば、その数も、4、16と増えていくのが世の常識(ならい)。
窓が16となりますと、驚きも、まだ序の口の65536。
窓が65536ともなりますと約2の後にゼロが19728個並びます。
これぞ、目出度きうさぎが延々と連なる幸を皆様にお届けせんとの姿に御座りまする
口上 窓辺うさぎ」
みなさま、明けましておめでとうございます。
上図は、今年の干支の兎にちなみ、窓から兎が「見える」、「見えない」の2通りの状態の組合せが窓数を直前の組合せ数に等しく増やしていくと、組合せの数が急速に大きくなる様子を表した図でして、今年の年賀状に掲載したものです。
全体の感じが歌舞伎調になりましたが、2010年暮れに起きました例の御曹司の殴打事件とは、まったく関係ありません。
この図案の方が時期的には、先だったのです。
とは言え、これを受け取られた方は、あるいは、ニヤリとされるかも知れません。
うさぎを御曹司に変え、「見える」、「見えない」を芝居に「出る」、「出ない」と読み替えると、奇しくも符合する部分ができてしまいました。
まったく、「初春の驚き」ですな。
目次に戻る
このような数は、以前、「DERIVE (デライブ) de ドライブ」で取り上げたことがあります。
再帰的帰納関数から導かれる数の例です。
 「ジャーン。おじさん。明けまして、おめでとうございます」
「ジャーン。おじさん。明けまして、おめでとうございます」
「お、ともちゃん。おめでとう」
「確か、関数の定義(2007年3月24日)の記事だったわ」
「さすが、「DERIVE de ドライブ」担当者じゃな」
「そこでの定義は、こんなことだったようね。n=2以上の整数として、f(n)=2^f(n-1)。なお、f(1)=2とする」
「アッカーマンというのは、ドイツの人の名前じゃな。ウィキペディアの記事を引用させてもらうと、
『Wilhelm Friedrich Ackermann。( 1896年3月29日 ~ 1962年12月24日)はドイツの数学者。計算理論の例として重要なアッカーマン関数を考案した』とある。
アッカーマン関数の定義じゃが、岩波数学辞典 第4版によると、自然数m,nの2変数関数として、次のように定義されているそうじゃ。
関数をAc(m, n) と書くとき、
Ac(0,n)=n+1
Ac(m+1, 0)=Ac(m, 1)
Ac(m+1,n+1)=Ac(m, Ac(m+1, n))」
「ふ~ん。DERIVEでやってみよう。
うへー。再帰的に定義すると、Ac(4,1)でもメモリー使い果たしてしまって計算できないよ!」
「自分自身を呼び出しているので、極めて、メモリーを使用する上に非効率的な計算となるのでな。
しかし、アッカーマン関数は、再帰的に呼び出さないと一般的に定義することができないのじゃ。
これを原始帰納的関数(いわゆる、ループ処理で記述することが可能な関数。たとえば、n!は、再帰的にも書けるがループ処理でも記述できる)でない帰納関数というそうじゃ。
さて、mを具体的な小さな値に固定して書き出してみると、
Ac(0,n)=n+1
Ac(1,n)=n+2、
Ac(2,n)=2n+3
Ac(3,n)=2^(n+3)-3
Ac(4,n)=2↑↑(n+3)-3
などとなる」
目次に戻る
 「ちょっと、おじさん。『↑ ↑』なんて記号、今まで出てきたっけ?」
「ちょっと、おじさん。『↑ ↑』なんて記号、今まで出てきたっけ?」
「これは、べき乗を拡張したもので、「クヌースの矢印表記」というものだそうじゃ。(ウィキペディアによる)
普通のべき乗、すなわち、2^n=2↑n などと書く。
↑↑は、具体的には、2↑↑n であれば、2の『超べき乗』で、2自身も含めて、2がn段重なったものじゃ
図で書けば、下図のようなものじゃ」

「そうすると、最初に出てきた、f(n)=2^f(n-1)。ここで、f(1)=2。は、f(n)=2↑↑n なのね」
「そう。だから、f(n+3)=Ac(4,n)+3とも、書ける。ただし、n>=0」
「なるほど。お正月の図に出てきた数は、一般的なアッカーマン関数の特別な場合の値とも言えるのね」
「クヌースは、↑↑の拡張もまた、定義している。
まず、x↑b=x^bと定義する。
次に、m>=2として、x↑m b=x↑↑・・↑b という表記を導入する。ここで、x↑m は、↑矢印が、m個並んでいるものとする。
たとえば、2↑3 3=は、2↑↑↑3。また、x↑m 1=x とする。
そして、x↑m n=x↑m-1 (x↑m (n-1))と再帰的に定義する。nは、1以上の整数じゃ」
「へー。
2↑↑3=2↑(2↑↑2)=2↑(4)=24=16 ということね。
そして、
2↑↑↑3=2↑↑(2↑↑↑2)=2↑↑(2↑↑(2↑↑↑1))=2↑↑(2↑↑(2))=2↑↑4=2↑(2↑↑3)=2↑16=2^16=65536
DERIVEで、x↑↑n=f(x,n)とすると、下図のように定義するのね。
ただし、ここのf(x,n)は、上のf(n)とは別のものだけど」
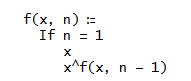
「従って、x↑↑↑n=g(x,n)と書くと、上のf(x,n)を使って、
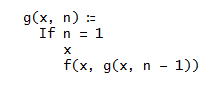
と、定義すればよい。
以下、↑の数に応じて、一つ前の関数を使って、再帰的定義自体は、可能じゃ。
ただし、↑↑↑以上は、定義からも明らかのように、xが整数でないといけない。
とはいうものの、
2↑↑↑2=g(2,2)=4、2↑↑↑3=g(2,3)=65536 であるが、2↑↑↑4=g(2,4)は、DERIVEで、メモリーオーバーとなってしまう。
実際、g(2,4)=2↑↑65536なのでな。念のため、言うておくと、これは、2^65536ではないよ」
「ゲゲゲ。その、クヌースって、一体、何者なのよ!」
「Donald Ervin Knuth は、米国の数学者(1983/1/10~)。コンピュータ科学の方面で、著名な学者じゃ」
「じゃ、x↑↑nとして、x=1~5、n=1~5までの1刻みの概数をDERIVEで計算して下図として掲げておくわ」
「この図だと、ベージュ色のx=2のn=1~5が、冒頭の兎の場合の数なんじゃな」

目次に戻る
「x=2の時、2↑↑nの値を2進数だと簡便に表せるのは分かるじゃろう」
 「は~い。
「は~い。
2↑↑n=2↑(2↑↑(n-1)) なので、まず、1を書いて、その後ろに0を2↑↑(n-1)個並べればいいのね」
「そのとおり。2↑↑5は、1の後ろに2↑↑(5-1)=2↑↑4=65536個のゼロを並べたものじゃ」
「つまり、2↑↑nは、前節の表を使うと、一つ前の2↑↑n-1個のゼロを並べれば、いいということね」
「2↑↑5は、10進数で表すと、年賀状の図柄の一部に取り込んだのを虫眼鏡で見てもらうと分かるじゃろうが、複雑じゃ。
しかし、2進数で表すと、1の後ろにゼロが65536個並んでいるだけじゃ」
「ということは、表に表していない、2↑↑6は、2進数で表すと、1の後ろにゼロが2^65536個≒2.003529930×10^(1.9728×10^4)
並んでいるということね」
「別の表し方だと、2を底とする、対数関数をlog2で表して、2重に使うと、log2(log2(2↑↑6))=2↑↑4=65536とも書ける。
これから、当然と言えば、当然なのじゃが、log2(log2(・・2↑↑n)・・)=1、ただし、log2は、n重に使う」
「そうすると、一般にmを正整数としたとき、m↑↑nは、mを底とする対数関数をn重に使うと、log m(log m(・・m↑↑n)・・)=1 ということね。
そして、m↑↑nを、m進数で記述すれば、1の後ろにm↑↑(n-1)個のゼロが並ぶことになる。
ま、これは、そもそもの定義からすれば、『あったり前でしょ』という声が聞こえてきそう」
「でも、何か、この表現を使うと、新しい見方が出てこんかとも思うのじゃがな」
目次に戻る
 「そのクヌースさんの↑↑の前の数値 2というのは、整数でなくて一般の正の実数でもいいのね?」
「そのクヌースさんの↑↑の前の数値 2というのは、整数でなくて一般の正の実数でもいいのね?」
「そう。アッカーマンの関数は、「数学基礎論」というものに現れるので、引数が自然数である場合を考えている。
しかし、クヌースの矢印標記の↑↑では、実数 xに対して、x ↑↑nを考えても差し支えない」
「というと、1.4 ↑↑nなどね」
「nが大きくなるとどうなるかな」
「DERIVEで計算すると、nを1~10まで、1つずつ変化させて、
[1.4, 1.601692898, 1.714163474, 1.780276017, 1.820322081, 1.845015801,
1.860409441, 1.870070491, 1.876159373, 1.880007075]
となる。
nを1~1000まで、100ずつ変化させてみると、
[1.4, 1.886663306, 1.886663306, 1.886663306, 1.886663306, 1.886663306, 1.886663306, 1.886663306, 1.886663306, 1.886663306]
となって、極限値は、1.88666・・のようね。でも、この場合は、DERIVEで極限値を計算させることはできないわ」
「実は、上の1.4は、数学セミナー(日本評論社:1986年10月号)の『グラハム博士 中学生に語る』という記事に現れている例なのじゃ。
同誌によると、
1.4<√2なので、1.4 ↑↑n<√2↑↑n=√2↑↑(n-1)^√2<√2↑↑(n-1)^2=√2↑↑(n-2)^2=・・=2 なので、
1.4 ↑↑n<2 という不等式が成り立つ。
ここの、最初の<は、1.4<√2≒1.4142・・からくる。
また、青色の部分の<は、n段ある√2のうち、一番上部の√2を2に置き換えたことによるものじゃ。
こうすることで、次の(√2)^√2を√2^2=2と置き換えることができる。
以下、芋づる式にすべて2となってしまうので、1.4 ↑↑n<2 が成り立つという訳じゃ。
なお、√2ではなくて、元の1.4のとき、ともちゃんが推測したその極限じゃが、後で述べるように、1.4^α - α = 0の根なのだ。
これは、数値的にしか計算できないが、2実根ある。この場合、小さい方の、α=1.886663306・・が極限値となる」
「じゃ、x↑↑nをx=1~1.8まで、xを0.1刻み、n=1~10まで計算してみるわ。
ジャーン。

不思議ね。xが1.5あたりから急速に発散してしまうみたい」
「今、x↑↑n=f(x,n)なので、nが無限大で有限な極限値αを持つ場合を考えよう。
定義から、極限において、α=x^αが成り立つはずじゃ。
これから、x=α^(1/α)となって、α=2のときは、x=√2となる。上で、1.4あたりで2に収束しそうなのと符合する」
「なるほど。でも、x=1.8のときには、発散してしまうことは、説明できないわね」
「そうでもないぞ。x=α^(1/α)のグラフを描いてみよう。
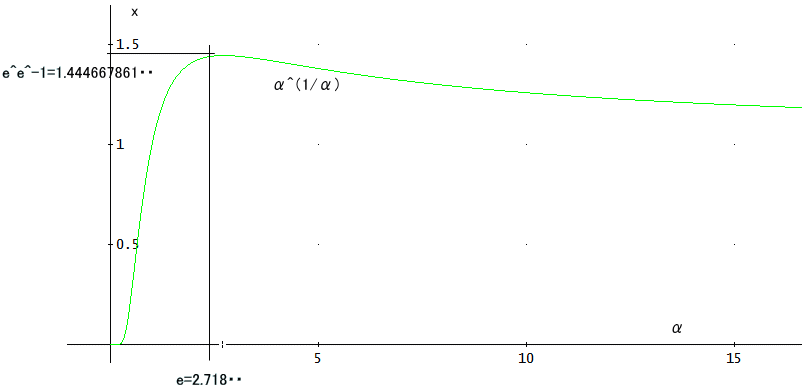
上図のようになる。
これから、f(x,n)が収束する場合、xの最大値は、e^e^-1=1.44467861・・であることが分かる。
√2≒1.41421356 や 先ほどの1.4などは、この値以下じゃな。
収束するxは、e^e^-1=1.44467861・・以下である必要があるので、x=1.8ではだめなのじゃ」
「ホント。
α^(1/α)の微分をゼロと置くと、α^((1 - 2α)/α)(1 - LN(α)) = 0、となるので、
これから、実根αを求めると、α=eであることがDERIVEで出てくるわね」
「グラフから、x<=1(α<=1.4446・・)では、x^α-α=0 の実根は、一つしかない。
しかし、1<x<e^e^-1≒1.44466・・の範囲では、上の方程式には、αの2つの実根があるのじゃな。
この、x=1というのは、α^(1/α)→1、α→∞のときの漸近線じゃな。
たとえば、x=1.3では、α≒1.4709889・・とα≒ 7.8570653・・と2実根がある。
ハッキリした証明が今は、思いつかないのじゃが、
1<x<=e^e^-1≒1.44466・・の間のxに対しては、x↑↑nのn→∞の極限は、方程式の2実根のうち、e≒2.718・以下の根となると予想できると思う」
「整数でないxについては、x↑↑↑nは、計算できないのね」
「そう。先のように、x↑↑n=f(x,n)は、xのべき乗をn個重ねたもので、xが整数でなくても計算できる。
しかし、↑が3本以上では、定義から、たとえば、x↑↑↑n=x↑↑(x↑↑↑(n-1))なので、↑↑の後ろの(x↑↑↑(n-1))が整数でないと、x↑↑()が計算できないのじゃ。
かっこ内が整数になるのは、xが整数の時に限られる」
目次に戻る
「まあ、しかし、人間の想像力というのは、恐ろしいものじゃ。
2↑↑↑3=2↑↑65536程度でも、想像を絶する大きさじゃというのに。
わしの感覚では、10^12=1兆程度になると、ほとんど、無限大というような感じじゃがな」
 「確かにね。
「確かにね。
Webで、調べてみると、兆の上は、
1京(けい)=10^16、1垓(がい)=10^20、1杼(じょ)=10^24、1穣(じょう)=10^28、などとなっているわ。
一番大きいのは、無量大数=10^68」
「ちなみに、10^100=1 googol(グーゴル)というそうな。Google(グーグル)の語源となったとのこと。
また、1グーゴルコンプレックス=10^10^100 というそうじゃが、これとて、2.2↑↑5<1グーゴルコンプレックス<2.3↑↑5<2↑↑6
じゃからな。
さっきの2↑↑65536などは、宇宙の大きさと比較しても桁違いに大きい数じゃ。
とはいうものの、形式的には、いくらでも大きい数の定義は、作れる。
しかし、『無限大』にくらべると、それすらも、無限小なのじゃ」
「宇宙の大きさは、宇宙が閉じていて、平坦であれば、概略、500億光年といわれているので、4.7×10^25 m程度に過ぎないものね」
「ははは、『・・に過ぎない』とはな。
まったくじゃ。クヌースの表記法などを見てしまうと、そんな感覚も分かるのう。
まして、『カントール』に始まる『集合論』では、自然数の無限大(有理数や『代数的数』(※参照)も同一レベル)の上のレベル(濃度というそうじゃ)に実数の無限大も出てくる。
そして、驚くことには、どんな無限大のレベルよりも大きい無限大のレベルを作り出せるそうじゃ。
上には上があるということかの。
今月は、お正月じゃから、無限大とまではいかなくても、気を長~くして過ごそうかな」
※代数的数:岩波数学辞典 第4版より要旨を以下に抜粋。
次数が有限な方程式、anx^n+an-1x^n-1+・・=0、の複素数までを含めた根を『代数的数』という。
ただし、ここで、anなどは、すべて整数とする。
代数的数には、定義から明らかのように、整数や有理数も含む上に、根号やべき乗などを含む√√(2-3√5)などや虚数単位を含んだ複素数も入る。
従って、私たちが日常、よくお目にかかる数は、たいてい、代数的数である。
一方で、π、eなどは、有理数でなく、無理数であるが、代数的数ではなく、『超越数』とよばれる数である。
実数の無限大のレベルが代数的数のそれよりも大きいことは、超越数の存在によるものであることが知られている。
しかし、与えられた実数が超越数であるか、否かを判定する一般的なアルゴリズムは、知られていない。
たとえば、オイラーの定数(C(DERIVEでは、γと書く)=Σ(k=1~n)1/k-LN(n)のn→∞の極限値≒0.5772156649・・)は、超越数であることはおろか無理数であることさえ証明されていない。
目次に戻る
今回もご覧いただき、ありがとうございました。
今年が皆様にとりまして、良き年でありますことを心より祈念いたします。
また、次回もこのページでお会いできますことを願っています。
目次に戻る