数式処理ソフト　DERIVE（デライブ） de ドライブ

４8．複素関数（３）（テイラー展開、ガンマ関数）

１．実関数のテイラー展開

「実関数 f(x)が範囲　－a=<x<=a で、無限回微分可能で、すべての導関数が正数Mより小さければ、f(x)は、当該範囲でテイラー展開が可能じゃ。
たとえば、exp(x)は、上記の範囲で無限回微分可能で、導関数もexp(a)より大きくなることはない。aに制約はないので、exp（x）は、実数の全域でテイラー展開が可能となるのじゃな。
実関数 f(x)をx＝x0で、n項までテイラー展開したときの剰余項は、Ln＝（x－x0）^（n+1）/（n+1）！×f⁽ⁿ⁺¹⁾（x0＋θ（x－x0））、
ここで、0<θ<1、そして、この形の剰余項をラグランジの剰余項と呼んでいる。
たとえば、f(x)＝1/（1+x） として、数式処理ソフト DERIVE（デライブ）で、x0＝0で、n＝5までテイラー展開して、誤差を見積もってご覧」

「f(0)＝－ x^5 + x^4 － x^3 + x^2 － x + 1＋L5、L5＝x^6/(θx + 1)^7、x＞0では、θ＝0として、
f(0.1)＝10/11≒0.9090909090、近似式では、0.90909 となり、｜近似値－真値｜＝1/1100000≒9.090909090×10^(－7)、一方、｜L5｜<10^－6　。
また、f(0.5)＝2/3、近似式では、21/32≒0.65625、｜近似値－真値｜＝1/96≒0.01041666666、一方、｜L5｜<0.015625　。
また、f(1)＝1/2＝0.5、近似式では、0 となり、｜近似値－真値｜＝0.5、一方、｜L5｜<1　。
そうね、これを見ると、Lnが、誤差の上限になっているということは分かるわね」

「そうじゃな。この級数は、一般項をa_nとすれば、a_n＝（－1）ⁿ×xⁿ であるので、近似式＝Σ（n=0～m）a_n＝1/(x + 1) － (－x)^(m + 1)/(x + 1)
従って、近似値－真値＝－ (－x)^(m + 1)/(x + 1) となる。これは、xが正だと、mにより正又は負になるのじゃが、－1＜x＜0の時は、負にしかならない。
下図が誤差の様子じゃ。



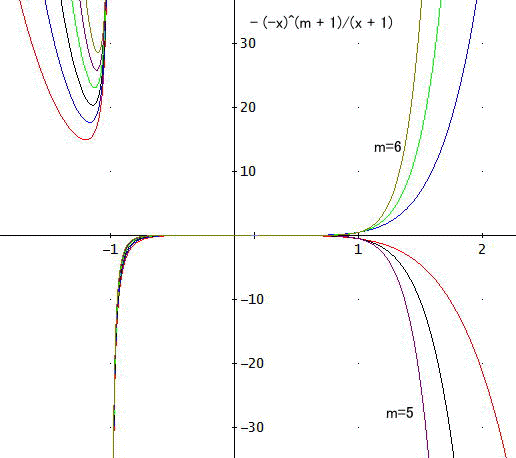
これを見ても、｜x｜<1の範囲内で、テイラー展開が可能であるということが実感できるの」

２．複素関数のテイラー展開

「第47回で正則関数、ω（z）は、何回でも微分できるという法則、ω^（n）（z）＝n！/（2π#i）∫ω（s）/（s－z）ⁿ⁺¹ ds が出てきた。
このため、正則関数は、正則点で実関数同様にテイラー展開できるだろう、ということは予想できる。
実際、テイラー（Taylor）の定理、ω（z）＝ω（z0）＋ω^（1）（z0）（z－z0）/1!＋ω^（2）（z0）（z－z0）/2!＋・・＋Ln が成り立っている。
ここで、Lnは、剰余項じゃ。このとき、z、z0は、Cで囲まれた正則領域内の点とする。
また、剰余項 Ln＝（z－z0）^（n+1）（1/2π#i）∫ω（s）/（（s－z0）ⁿ⁺¹（s－z））ds において、Ln→0になれば、この無限級数は、収束する。
そのとき、z0を中心としたこのテイラー級数が収束する最大の｜z－z0｜をz0でのωの収束半径と言うのじゃな」

「実関数のテイラー展開と同じようなものね。でも、実関数で「収束半径」って用語は出てきたっけ？」

「実関数では、「収束半径」とは言ってないのう。「テイラー展開可能な範囲」とか、「・・の範囲でテイラー展開可能」とか、言っているようじゃな。
ω（z）＝1/（z＋1）でさっきのように調べてご覧」

「まず、1/（z＋1）は、正則関数である 1/zでz → z＋1としたものなので、やはり、正則関数である。
これは、コーシー・リーマンの関係式からも、直接、確認することも出来るし。
特異点は、孤立特異点 z＝－1 が1位の単極となっているのね。
次に、特異点以外のzでは、ω^（n）（z）＝n！/（2π#i）∫ω（s）/（s－z）ⁿ⁺¹ ds ＝n！/（2π#i）∫1/（（s+1）（s－z）ⁿ⁺¹） ds から、
テイラー展開する点を原点z＝0として、積分内を部分分数に分解すると、（－1）ⁿ⁺¹/(1+s)＋Σ（k＝0～n）（－1）^k×s^k/sⁿ⁺¹ となることが分かる。
ここで、s＝r exp（#i θ）として、r < 1、θ＝0～2πで積分すると、上記の第1項は、ゼロとなり、また、第2項の和は、k＝n、すなわち、1/sの項のみがゼロでない。
これにより、ω^（n）（0）＝n!×（－1）ⁿ である。これは、1/z+1を直接、n回微分して、z＝0とおいた結果と同一である。
従って、1/1+z＝Σ（k＝0～∞）（－1）^k×z^k 、ただし、｜z｜<1 でないと収束しないので、z＝0での収束半径は、1である」

「ふ～ん。第1項、1/（s+1）が積分するとゼロになるのは、どうしてじゃな？」

「1/（s+1）は、s＝－1がただ一つの特異点で、s＝0を中心とする半径が1より小さい円内では、正則関数だから、コーシーの積分定理から、この線積分はゼロとなるというわけ」

「なるほど。では、第2項のΣ内の1/s以外がゼロとなるのは、どうしてじゃな？」

「これは簡単。k＜nでは、1/s² などとなるので、s＝r exp（#i θ）から、ds＝r #i exp（#i θ）dθと掛けたとき、定数×exp（－#i θ×m）となる。ここで、m＝1～の整数。積分は、0～2πで行うので、これらは、ゼロとなるわ」

３．複素級数の収束判定

「複素関数の数列を考えた時、第n部分和＝S_n＝Σ（k＝0～n）f（k，z）とすると、lim（ n→∞）S_n→Sが存在するならば、Sを無限級数の和というのじゃな。
級数の収束を判定する方法がいくつかある。
まずは、各項 f（k，z）がz→∞で、ゼロに収束する必要がある。逆は、成り立たないので、各項がゼロに収束しても、級数が発散または振動しないとは限らないがの。
なお、Σ（k＝0～∞）｜f（k，z）｜が収束するときを、「絶対収束」といい、絶対収束はしないが、Σ（k＝0～∞）f（k，z）は、収束する時を「条件収束」するというそうじゃ。絶対収束する級数では、各項の順序を入れ替えても級数の和は変わらない。
絶対収束の判定によく使われているのが「比検定」という方法じゃ。
lim （k→∞）｜f（k+1，z）/f（k，z）｜＜ 1 のとき、この級数は、絶対収束する。1より大きいときは、発散する。1と等しいときは、この方法では、判定出来ない。
前節の級数、Σ（k＝0～∞）（－1）^k×z^k では、
lim （k→∞）｜f（k+1，z）/f（k，z）｜＝lim （k→∞）｜z｜＝｜z｜なので、｜z｜＜ 1 で絶対収束することが分かる」

４．ガンマ関数

「関数　ω＝1/√（1+z²）をz＝0の回りで、テイラー展開してみよう。
1/√（1+z）＝Σ（n＝0～∞）(－1)^n(n － 1/2)!/(√πn!) ×z^n から、1/√（1+z²）＝Σ（n＝0～∞）（(－1)ⁿ (n － 1/2) !/(√πn!)） ×z²ⁿ
ここで、比検定を使ってみると、lim （n→∞）｜f（n+1，z）/f（n，z）｜＝lim （n→∞）｜(－ z^2(2n + 1)/(2(n + 1))｜＝｜z²｜
これより、｜z｜＜ 1ならば、絶対収束することが分かる」

「ちょっと、ちょっと、おじさん！　（n－1/2）！って、何なの？」

「これは、ともちゃんも知っている階乗を拡張したものじゃよ。階乗の定義は何じゃな」

「n!＝1×2×3・・×n でしょ。もっとも、0! は、1と定義するけど」

「うん。そうじゃな。しかし、このままでは、n が半整数の階乗は定義されていないので、求められない。
そこでじゃ、「数学の本質は拡張にあり」、に従って、階乗の定義を拡張することにしたのじゃな。
今、xを実数として、f(x+1)＝x×f(x)、f(1)＝1 となる関数を考える。これは、x＝1、2・・で階乗の定義を満たしている。
すなわち、階乗を拡張したものになっている。しかし、このままでは、実数はおろか、半整数の階乗の値もどのように定義していいか分からない。
さて、天下り式じゃが、x>= 0の実数 として、定積分 ∫（t＝0～∞）（t^x×exp（－t））dt 考える。
これを部分積分すると、0＝x∫（t＝0～∞）（t^x－1×exp（－t））dt－∫（t＝0～∞）（t^x×exp（－t））dt なので、
g(x+1)＝∫（t＝0～∞）（t^x×exp（－t））dt とすれば、上記の関数方程式 g(x+1)＝x×g(x) を満たす。
さらに、x＝0として直接計算すると、g(1)＝1 となり、f(x)＝g(x)と置いてよいことが分かる。
このように定義した関数を「ガンマ関数」という。すなわち、Γ（x+1）＝∫（t＝0～∞）（t^x×exp（－t））dt、
xが正の整数では、Γ（n+1）＝n! となるのじゃ。
こうすると、x＝1/2では、Γ（3/2）＝√π/2＝（1/2）！、Γ（5/2）＝3/2×Γ（3/2）＝（3/2）！＝3√π/4、・・と半整数の値も求められるのじゃな」

「へー。だけど、Γ（1）より、xが小さいときの値は決まらないわね」

「実は、x>－1 であれば、∫（t＝0～∞）（t^x×exp（－t））dt で計算可能なので、Γ（1/2）＝（－1/2）！＝√πとなって、負の階乗も定義できる。
また、関数関係式を使って、Γ（－1/2）＝－2Γ（1/2）＝－2√πなどと負の時のガンマ関数の値も定義できる。
定義できないのは、ゼロと負の整数のみじゃ。
ちなみに、ガンマ関数のグラフは、下記のようになる。



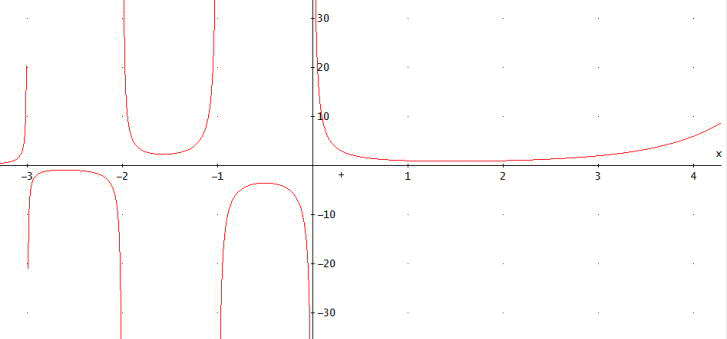
「DERIVEでは、下部のパレットから、Γを選べば、よいのね。
そうそう、階乗と言えば、第10回で、ln（100!）の近似値を計算したね」

「そうじゃったな。その際は、近似値≒363.8196036、真値＝LN（100！）≒363.73937555556349014 と 3桁目までしか合わなかったが、今回、新しい観点から見直すと、もう少し近似度を上げられるのじゃ。
なお、ガンマ関数の複素関数としての扱いは、後日の宿題として、ここでは、被積分関数を近似関数で置き換えることを試してみよう。
まずは、被積分関数、t^x×exp（－t）がt＝xで極大値をとるので、これを、a×exp（－b（t－x）^2）で置き換えることを考える。ここで、a、bは、xの関数とする。
最大値＝exp（－x）x^x から、a＝exp（－x）x^x 、また、近似関数のtによる1階微分のt＝xでの値は、自動的にゼロとなる。
そこで、t^x×exp（－t）の極大値における2階微分係数に一致するように近似関数をtで2階微分して、bを定めると、b＝1/2xとなる。
これらより、近似関数は、exp(－ 3x/2 － t^2/(2x) + t) x^x となるので、t＝0～∞で定積分すると、
積分値≒exp(－x)x^x(√2√π√xERF(√2√x/2)/2 + √2√π√x/2) となるが、xが大きいときは、ERF(√2√x/2)≒1 としてよいので、
積分値は、簡単化されて、√（2πx）exp(－x) x^x となる。
積分値の自然対数は、(x + 1/2)LN(x) + LN(2π)/2 － x であり、x＝100に対して、363.7385422 を与える。これは、真値363.73937555556349014と比較して、5桁目まで一致している。
ちなみに、第10回で記載した正確な漸近展開である、n！≒√（2πn）×（n／e）^n×（1＋1／（12n）＋1／（288n^2）・・）と比較すると、第1項まで一致していることが分かるじゃろう」

「ほんと、びっくりだね」

「ついでに言うと、Γ関数の積分表示で、変数変換すると、様々な表現が得られる。
たとえば、√t＝uと置くと、Γ（x+1）＝2∫（u＝0～∞）exp（－u²）u^（2x+1）du が得られる。
また、exp（－t）＝uと置くと、Γ（x+1）＝∫（u＝0～1）（－LN（u））^x du も得られるのじゃな。
ただし、前出のような近似計算には、ちと、役に立たないような感じじゃな」

「DERIVEでx＝n（正整数）として、二つ目の式∫（u＝0～1）（－LN（u））ⁿ du を計算すると、ちゃんと、n! となるわ！」

「DERIVEでは、何度でも試行錯誤的に簡単に計算できるので、面倒がらずにいろいろとやってご覧」

最終更新日　2008/10/24