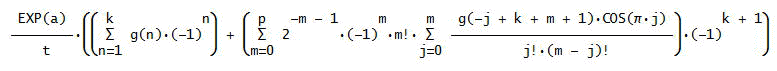数式処理ソフト　DERIVE（デライブ） de ドライブ

４５．積分（５）（高速ラプラス逆変換２）

１．FILTの式の見直し

「数式処理ソフト DERIVE（デライブ）の前回の記事では、テスト関数 F（s）＝1/(s^2+1) を元に、f（t）（これは、原関数：sin（t））の近似式として、
f（t）≒exp（a）/t×｛Σ（n=1～k）（－1）ⁿF_n＋Σ（m=0～）（－1）^（k+m+1）Δ^mF_k+1/2^(m+1)｝　－－（１）
とした。そして、ともちゃんにDERIVEで計算してもらったのじゃったな」

「そう。だけど、ものすごく、ゴチャゴチャした式になってしまったわ。もう少し、すっきりとしないのかな」

「そうじゃな。（１）式のとおり、階差を再帰的定義関数で求めるのは、無駄が多い。
これは、「BASICによる高速ラプラス変換（細野敏夫著：共立出版：1984年）」（以下、「細野本」という。）にも、また、以前、引用した森口先生の本（「森口本」という。）にも注意されていることじゃ。
一般に数列、g（n）、ただし、n＝1～を考える。Euler変換を開始するnを、k+1と固定すると、第p階差までの式は、次のように書ける。

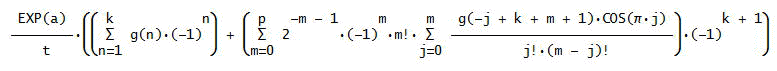
DERIVEの式をコピーすると、上と同じことじゃが、
EXP(a)/t(∑(g(n)(－1)^n, n, 1, k) + ∑(2^(－m － 1)(－1)^mm!∑(g(－j + k + m + 1)COS(πj)/(j!(m － j)!), j, 0, m), m, 0, p)(－1)^(k + 1))　－－（２）
となる」

「じゃ、この式を使って、もう一度、計算してみるよ。
まずは、a＝3、k＝10、p＝3としてみよう。おなじみのsin（1）≒0.8411141054　、真値は、0.8414709848 なので、3桁まで、一致は、前回と同一ね。末尾の数値が少し違うのは、丸めの関係かしらね。
次に、a＝6、k＝10、p＝8とすると、sin（1）≒0.8414700937 で、6桁目まで一致する。
あ、今、気がついたんだけど、aの値を変えたときは、g（n）のaの値を置換してから、DERIVEの入力－関数の定義から関数を定義し直さないといけなとのね。前の定義内容が残っているんだ！」

「そのようだの。それと、関連するが、（２）式の計算前にg（n）のaの値をセットしてから行った方が便利で早いことが分かったの。
ただ、一つ、問題は、あるのう。（２）式で計算すると結果の表現中に、10^500などの途方もない大きな数字がぞろぞと出てきて、個別の値の計算は出来てもDERIVEでグラフが自動的に描けないことじゃ。これは、問題じゃな」

「それとー。今気がついたんだけど、「細野本」と「森口本」では、差分の式の符号やEuler変換の式が違う！」

「なーるほど。これは、わしとしたことが気がつかなんだな。「森口本」では、標準的な、差分（前進差分）、すなわち、Δa（n）＝a（n+1）－a（n）を考えているので、k+1項目からEuler変換する場合の部分和は、a（k+1）/2－Δa（k+1）/4＋Δ²a（k+1）/8－＋・・となっている。（森口本－P38）
同様に、岩波数学辞典でも、このように記載されている。
ところが、「細野本」では、「差分」DをDv（k）＝v（k+1）＋v（k）と定義していることと、Euler変換の部分和を、v（k+1）/2＋Dv（k+1）/4＋D²v（k+1）/8＋・・と記載している」

「どうしてなのかな。ミスプリかしら？」

「これはじゃ。細野本では、v（k）＝（－1）^k×a（k）のように、vに符号を含めて、考えているのじゃな。このようにすると、双方、同一の結果になることは、少し、計算すると、分かるじゃろう。細野本は、1984年出版時、BASICでプログラムを書いているので、できるだけ、余分なメモリーを使わずにできるように工夫したんじゃと思う。
ただ、数学で普通に「差分」といったとき、Dv（k）＝v（k+1）＋v（k）では、わかりにくいと思うので、ここでは、一般的な記法に従っておこう」

２．Euler変換公式の導出

「森口本に従って、簡単に、Eulerの式を導いてみよう。
以下、級数の各項をa（n）で表す。ただし、符号は式中に明示して表示して、n＝0～とする。
まず、「ずらし演算子」Eを、E×a（n）＝a（n+1）と定義する。また、E^k×a（n）＝a（n+k）とする。
一方、Δa（n）＝a（n+1）－a（n）＝E×a（n）－a（n）＝（E－1）×a（n）なので、Δ＝E－1と考えることができる。
そこで、交代級数、S＝a（0）－a（1）＋a（2）－＋・・を考えると、S＝a（0）－E×a（0）＋E²×a（0）－＋・・＝（1－E＋E²－＋・・）a（0）
ところで、Eの「級数」が収束すると仮定すれば、初項 1、公比（－E）であるので、S＝1/（1＋E）×a（0）
ここで、先のΔ＝E－1から、E＝1＋Δより、S＝1/（2＋Δ）a（0）＝（1/2）×1/（1＋Δ/2）×a（0）＝（1/2－Δ/4＋Δ²/8－Δ³/16＋－・・）×a（0）。
となって、Euler変換の式が「導出」された」

「へー。びっくり。まさに「演算子」の活躍ね」

「上のは、発見法的な導出法であって、もっと、数学的な導出は、森口本のP48以降に記載されているので、あとで、見てご覧」
※青字部分の数値が間違っていました。お詫びして訂正いたします。（2013/2/7）

３．Euler変換の収束性と誤差

「実は、今回の例で取り上げた、sin（t）関数は、tの実数域（今考えているのは、t>=0だけであるが）で最大値±1をとる周期2πの関数なので、tが大きくなると、Euler変換の収束条件を満たすことはできないのじゃな。
それで、第44回のグラフのように、t－>大で、近似値と真値との関係は破綻（近似値がゼロになる）してしまう。
Euler変換の収束性については、「完全に単調な数列a（n）が0に収束すれば、Euler変換した級数の和も公比1/2の級数と同じかまたはそれよりも早く収束する」ことが知られている。（森口本　P53）
これを今回の近似式に当てはめて考える。
F（s）のs＝a＋i（n－1/2）πとしたときの、IM（F（s）を、必要な精度（これはaで決まるので、3桁なら3、6桁ならば6とする）により、aの値を定め、求めたいtの範囲（0～T）について、適当な刻み幅でnに関する関数の数列を作成する。
そして、各数列を元に横軸をnと考えて、グラフを描き、明らかに単調に減少するあたりのnを求め、このnを近似式の最初の和のkとする。
（※この部分は、細野本による。なお、同書では、もっと、緻密な誤差解析を行っている）
たとえば、精度3桁としてa＝3とし、求めたいtの範囲は、t＝0～10、20、30まで求めたいとすれば、次のようになる。

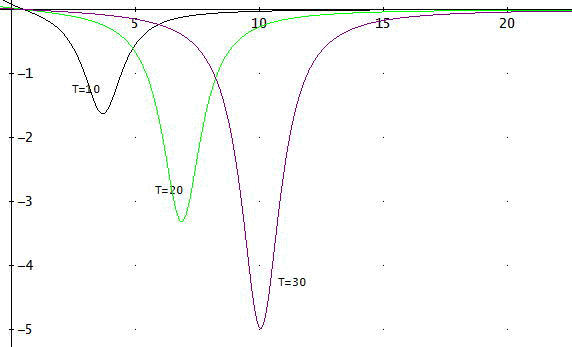
　これによれば、T＝10であれば、kは少なくとも>=5、T＝20ならば、k>=10、T＝30でk>＝15とすれば、良いであろうことが分かる。
図1　a＝3、k＝5、p＝5のときの近似式（ドットで表示：0.1単位）とsin（t）の曲線

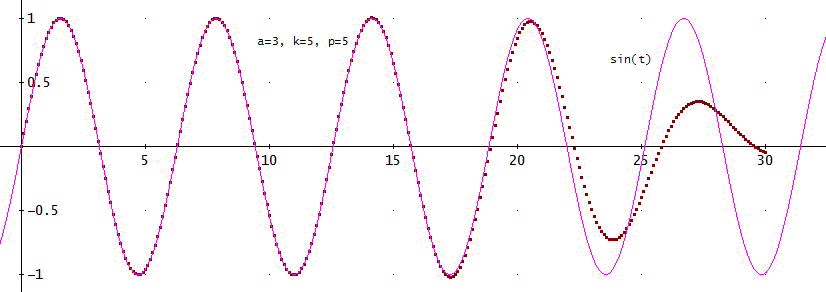
図２　a＝3、k＝10、p＝5のときの近似式（ドットで表示：0.1単位）とsin（t）の曲線

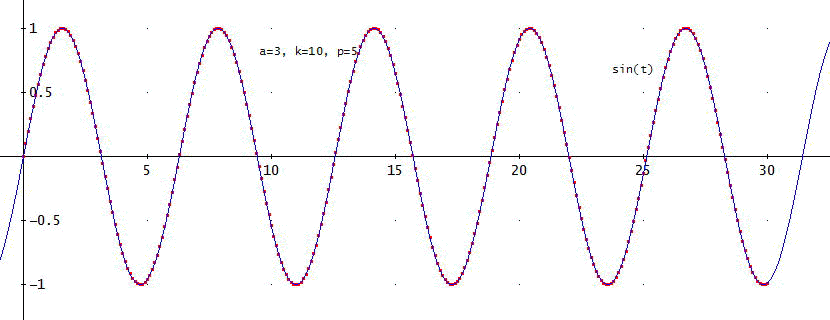
　aを精度として、階差は、+2の第5階差までとってみた。グラフで見ると、まあまあ、問題なく満足しているのう」

「この近似式のドットは、どうやって描いたの？」

「これはじゃ。近似式を元に、DERIVEのメニューから、解析－数列の作成と選んで、tの範囲として、0～30、刻み幅を0.1単位で、近似式の数列を作成する。
この作成した数列は、ベクトルとなるので、それをvと置く。このベクトルから、［0.1×（k－1），v ↓k］として、2次元のベクトルを定義する。
そして、再度、数列の作成から、kを1～301までで作成する。これは、縦長の長いベクトルとなるが、それをプロットするとドットの集まりになるのじゃ」

「チョー面倒ね。もう少し、簡単な方法はないの？」

「今のところ、思い浮かばんのう。この方法もいろいろと実験して見つけたのじゃよってに、DERIVEの推奨の方法かどうかは分からん。
ともちゃんもやってみてチョー」

「・・・」

４．グラフ

「前節でなんとか、苦し紛れじゃが、近似式のグラフを描く方法が見つかったので、ともちゃん、1節の近似式のグラフを描いてご覧」

「じゃ、a＝3、k＝10、p＝3の場合を（２）式を元にしてグラフ化してみるよ。

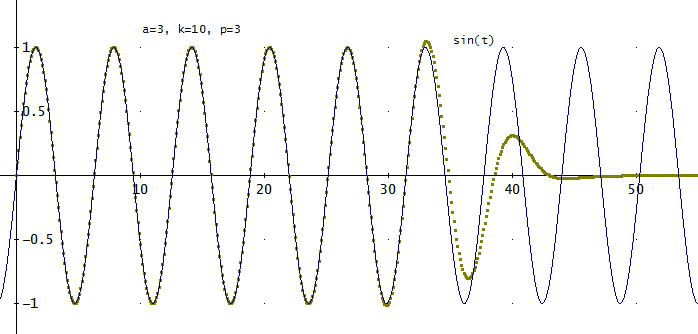
　なるほど、前節のk＝5では、真値から、t＝25付近で明らかに外れるのに対して、こちらは、35付近だわ。
kを増やした効果が出ているのね」