

新年のご挨拶
ベジェ曲線とは
座標変換との関係
同次座標
n=1のとき
n=2のとき
n=2のとき(再)
n=3のとき
n=一般でxが等分割のとき
曲線の近似と制御点の選択
2次の場合、4分円に完全に一致はできない
2次の場合、4分円に近似的に一致(1)
2次の場合に4分円に近似的に一致(2)
4分楕円の近似(1)
4分楕円の近似(2)
終わりにあたって
みなさま、明けましておめでとうございます。
今年もよろしくお願いいたします。
目次に戻る
さて、当教室のコースに「Photoshop CS」、「Photoshop CS2」コースがあります。
この中で、なめらかな曲線を引くため、いわゆる「パス機能」を使う際に用いられているのが、今回の主題の「ベジェ曲線」です。
ベジェ曲線とは、フランスの工学者である「Pierre Bezier」氏の創案になるもので、2点間を結ぶ曲線の表示方法の一種です。
n次のベジェ曲線の定義は、フリー百科事典である「ウィキペディア」によれば、2点をr(0)とr(n)として、制御点をr(1)~r(n-1)とすれば、
r=ΣnCi ti (1-t)n-i r(i) 、ここでi=0~nであり、パラメータ tは、0~1を動きます。
なお、nCiは、n!/((n-i)!i!)を表し、rは、位置ベクトルです。
定義式から明らかのようにnの如何に関わらず、t=0で始点となり、t=1で終点となります。
目次に戻る
ベジェ曲線の定義式は、制御する点の位置ベクトルのみからなっているため、座標軸の取り方には、直接、依存しません。
2次元平面では、平面を複素平面と同一視して座標ベクトルr(i)を複素数と考えこともできます。
このとき、位置の平行移動は、r(i)に任意の複素数zを加えることであり、回転・伸縮は、zをかけることですが、ベジェ曲線rは、定義式がr(i)について線形ですのでこのような座標の変換操作に対して同型に変換します。
つまり、r(i)+zに対して、rは、r+zと変化し、r(i)×zに対して、rは、r×zと変化するのです。
2次元に限らず、3次元の場合も含めて、このような座標の平行移動や回転は、一般にアフィン変換といわれています。
目次に戻る
本稿の主題とは、少し、離れますが、アフィン変換の話が出ましたので、コンピュータグラフィックスで用いられている「同次座標」について、触れておきましょう。
以下では、一般の位置ベクトルを考えます。
2次元については、前節のように複素数と見なして整理することも可能ですが、3次元に拡張することを考えた場合も含めて不便な点があります。
(注:3次元の場合に複素数の拡張である四元数を使用する方法もあります。蛇足ですが、WEBで検索すると更に八元数や、なんと!十六元数かもあるようです)
一つは、移動と回転が異なった演算操作を要求する点です。すなわち、移動については、加算、回転については、乗算というようにです。
もう一つは、無限遠の表現方法です。座標変換によっては、変換後の座標が無限大になることがあり得ます。
普通の座標では、無限遠点を表現できないので、ここが不便です。
そこで、よく用いられているのが「同次座標」という方法です。
これは、2次元の場合、[x,y]’(’は、転置を表す)という座標を[u,v,w]’という3つの座標で表そうというものです。
x=u/w、y=v/wという関係があります。
これによりw=0の場合として、無限遠を表すことができます。
移動については、移動量を[a.b]’とした場合に[x+a,y+b]’ですが、これをT*[u,v,w]’として、T=[[1,0,a][0,1,b][0,0,1]]という行列です。
実際は、このような形です。

更に回転の場合は、変換行列は、

とすれば、よいわけです。
また、伸縮は、x方向にα倍、y方向にβ倍として、

のように変換行列をとります。
このようにすると座標変換を行列演算の積のみで表現することができます。
元の座標に戻す場合は、前述のようにx=u/w、y=v/wの関係を使います。
3次元の場合は、同次座標は、4つの数値の組を用いて表現できます。
目次に戻る
ベジェ曲線に話を戻しましょう。
1次のベジェ曲線は、r=r(0)(1-t)+r(1)t となります。
この式からも2点を結ぶ直線であることは、明らかではありますが、2006年11月の今月のご挨拶で取り上げましたDeriveで計算をしてみましょう。
DERIVEでの便宜上、2点の座標値を、(x1,y1)、(x2,y2)とすると
x=x1(1-t)+x2t
y=y1(1-t)+y2t
となります。
まずは、DERIVEのオプションのモード設定の入力で「連続した文字列を1変数と見なす」にしておきます。
次にメニューの「解く」から連立方程式を選択して次元を2とします。
前述の2つの式を入れて、変数をxとyと置いて方程式を解きます。すると、
x(y1 - y2) + y(x2 - x1) + x1y2 - x2y1 = 0
とxとyの関係式が求まります。これは、x2≠x1のとき、(x(y1 - y2) + x1y2 - x2y1)/(x1 - x2) となりますので、2点を結ぶ直線であることが分かります。
パラメータ表示の都合のよいところは、x2=x1のような場合でもx2≠x1のときとまったく同様に扱えるという点です。
目次に戻る
2次のベジェ曲線は、r=r(0)(1-t)2+2r(1)t(1-t)+r(2)t2 となります。
1次の場合と同様に座標を使ってみましょう。ここでも添え字を1から始めるようにします。
同様にDERIVEで計算してみましょう。
しかし、n=1の時と異なり、定数がx1、y1、x2、y2、x3、y3と6個もあるので煩雑になります。
そこで、まずは、始点(x1、y1)を原点として、終点(x3、y3)を(1、0)とすることにします。このようにしても特徴は、失われません。
x = t(2x2 - t(2x2 - 1))
y = 2ty2(1 - t)
ここからtを消去して、xとyで整理すると
となります。
上式が正しいことは、x及びyの式を代入すると恒等式となることから分かります。
x、yの連立方程式から上式を導くには、いろいろな方法があります。
直接的には、DERIVEでxの式からtを求めて(2根あります)、yの式に代入して整理するという方法ですが、式の途中で平方根号が出てくるため整理するときに機械的には、いきませんし、2根の扱いの吟味が面倒です。
2つめの方法は、要領のよい方法です。あらかじめ、xとyの2次式であると仮定して、すなわち、x2+ay2+bxy+cx+dy+e=0とおき、x,yの式を代入し、この式がtの任意の値で満足されなければならないことからt=0、1、0.5等の値を未知数の数だけ代入して、それらの連立方程式から、a、b、c等を求める未定係数法的な方法です。
3つめの方法は、2つめの方法でtの任意の値のところというのが、今ひとつ、数学的でないような感じなので、x2+ay2+bxy+cx+dy+e=0をtの式と見て、tで次々と微分してt=0と置き、未定係数を求める方法です。
いずれの方法でも同じ式が求まりました。
今回、もっとも、簡単なのは、2番目の方法でした。
目次に戻る
前述のケースでは、始点を原点、終点を(1,0)として計算を簡易化しました。
試みに、DERIVEで上述の条件を外した一般のケースが計算できるか求めてみました。
未知係数についての5元連立方程式を解くことになります。
やあー。DERIVEは、賢いですね。一瞬のうちに係数を求めてしまいましたよ。
元の式に代入してみると、次のようになります。
上式は、複雑ですが、x1=0、y1=0、x3=1、y3=0とすると前節の式になります。
目次に戻る
3次のベジェ曲線は、r=r(0)(1-t)3+3r(1)t(1-t)2+3r(2)t2(1-t)+r(3)t3 となります。
2次の場合と同様に考えるのですが、始点を原点に、終点を(1,0)にしてみます。このようにすると、
x = t(t(3x2 - 3x3 + 1) + 3t(x3 - 2x2) + 3x2)
y = 3t(t - 1)(t(y2 - y3) - y2)
であり、一般の3次式を仮定すると、x3 + a1x2 + a2x + a3x2y + a4xy2 + a5y3 + a6y2 + a7y + a8 = 0となりますので、xとyの式を代入して、2次の場合と同様に未知係数を定めようとすると、本質的には6元連立方程式を解くことになり、DERIVEでも、容易に解が求まりません。
そこで、2次式の場合の3番目の方法、すなわち、tで微分していく方法では、どうかと試みると10秒程度で解が求まりました。
しかし、ここには、さすがに貼り付けることは、無理(無駄?)のような長~い式となります。
そこで、制御座標である、x2=1/3、x3=2/3として解を簡易化してみましょう。
となって、びっくりするくらい、簡素な形になります。
目次に戻る
前節で制御点のx座標を始点と終点との間で等分すると、ずいぶんと式が簡素化されることが分かりました。
そこで、ここでは、最初からこのように置いてみました。始点を原点に、終点を(1、0)としています。
xの定義式から制御点のx座標が等分割であるとすると、x=Σn!i/(n(n-i)!i!)(1-t)n-itiとなります。
ここで、iは、0~nまで動きます。
i=0では、初項がゼロとなるため、この和は、i=k+1として、添え字をkに変更して整理すると、t Σ(n-1)!/((n-k-1)!k!)(1-t)n-k-1 tk となります。
そして、Σの部分が((1-t)+t)n-1=1 であることから、結局、x=tということが分かります。
そうしますと、yの式は、y=Σyi nCi (1-t)n-i ti となりますが、(i=0~n) yiがi=0と1でゼロであることから、結局、y=Σyi nCi (1-x)n-i xi となりました。
ここでi=1~n-1を動きます。
n=3の場合は、 y = 3x3(y2 - y3) + 3x2(y3 - 2y2) + 3y2xとなりますので、前節の式と一致します。
目次に戻る
これまでは、始点と終点が与えられて、その間をつなぐベジェ曲線を求めてきましたが、ここでは、視点を変えて、始点と終点とその間をつなぐ曲線が与えられた場合に制御点をどのように選択するかという問題を考えてみましょう。
1次曲線(直線)では、制御点がありませんので、n>1として考えます。
目次に戻る
代表的な2次曲線である円(4分円)を取り上げましょう。中心を原点に、半径を1とします。
始点(0、1)と終点(1、0)をつなぐ4分円は、x2+y2=1、x、y>=0です。
一方、ベジェ曲線でn=2の場合を書き下すと、制御点を(x2、y2)として、
x = t(2x2 - t(2x2 - 1))
y = (1 - t)(t(2y2 - 1) + 1)
となります。この式がx2+y2-1=0 を t(=0~1)の値にかかわらず、満足する(x2、y2)があるかと調べてみますと、それは、ないことが分かります。
目次に戻る
前節では、4分円の場合に完全に一致は、無理ということが分かりましたが、どの程度、近似させることができるかを調べてみましょう。
残差=x2+y2-1=t4(4x22 - 4x2 + 4y22 - 4y2 + 2) - 4t3(2x22 - x2 + 2y22 - 3y2 + 1) + t2(4x22 + 2(2y22 - 6y2 + 3)) + t(4y2 - 4)
ここで、対称性から考えて、制御点は、y=xの線上に存在する場合が残差がもっとも小さくなると考えられますので、y2=x2と置きます。
残差=t4(8x22 - 8x2 + 2) - 4t3(4x22 - 4x2 + 1) + 2t2(4x22 - 6x2 + 3) + t(4x2 - 4)、なお、残差は、t=0及び1でゼロになることが分かります。
残差をtの関数と見て、tの微分係数がゼロとなるtの値を調べます。tが極値を取るのは、次の場合です。
残差(ケース1)の極値をゼロにするx2=1、残差=2t4 - 4t3 + 2t2、残差の最大値は、t=1/2で、1/8=0.125となります。
残差(ケース2)の極値をゼロにする場合は、上記と同一となります。
最後のケースでは、x2=√2-0.5、残差=t4(24 - 16√2) + t3(32√2 - 48) + t2(30 - 20√2) + t(4√2 - 6)、最大となるtの値は、t=1/2±√2/4( 0.8535533905 または 0.1464466094
)のときで、残差の最大値は、√2/4 - 3/8≒-0.02144660940 となり、ケース1及び2よりもかなり小さく押さえられることが分かります。
下図は、残差=t4(24 - 16√2) + t3(32√2 - 48) + t2(30 - 20√2) + t(4√2 - 6)のグラフ。横軸は、t
従いまして、4分円の残差を小さくする最良の近似としましては、
x = - t(2t(√2 - 1) - 2√2 + 1)
y = (1 - t)(2t(√2 - 1) + 1)
が得られました。
この場合の実際のグラフを下図のようにDERIVEで描かせてみました。
×印は、制御点(x2=y2=√2-0.5)の概略位置をあらわします。
なお、この場合の弧長は、下記のように約1.562417125となり、真の弧長であるπ/2≒1.570796326との相対誤差は、約 -0.53%となります。
目次に戻る
前節では、始点と終点での接線の傾きが真円の場合と異なってしまいます。
これを始点では、傾きゼロ、終点では垂直とするの前節のケース1の場合です。
このとき、制御点(x2,y2)は、(1,1)であり、前節で記載したように残差の最大値は、1/8となります。
なお、残差のグラフは、下図のようになります。
また、このとき x=t(2-t)、y=(1+t)(1-t)で表される近似曲線は、下のようになります。ここで×は、制御点の概略位置を表します。
こちらの場合の弧長は、1 - √2LN(√2 - 1)/2≒1.62322524であり、真の弧長との相対誤差は、約3.3%となります。
目次に戻る
4分円と同様に楕円(の1/4)の近似を考えてみましょう。
円の場合と同様に計算することもできますが、変換によって円の場合の式と制御座標を楕円に写してしまいましょう。
ここでは、楕円の離心率 扁平率をeとして(0=<e<1)、長軸をx方向にとり、その長さを1、短軸をy方向にとり、その長さを1-eとしましょう。
このとき、4分円の近似(1)では、 x = - t(2t(√2 - 1) - 2√2 + 1)、y = (1 - t)(2t(√2 - 1)
+ 1) でしたが、これのy方向のみ(1-e)倍とします。
また、制御座標y2も同一の係数をかけましょう。
すると
x = - t(2t(√2 - 1) - 2√2 + 1)
y = (1 - t)(2t(√2 - 1) + 1)(1-e)
x2=√2-0.5、y2=(√2-0.5)(1-e)
となります。離心率 扁平率 eを0から0.9まで0.1ずつ変化させて、グラフを描いてみました。
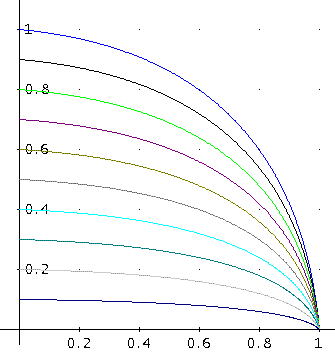
これらの楕円の正確な弧長は、第2種不完全楕円積分E(k,φ)=∫√(1-k2sin2θ)dθ、積分範囲は、0~φを用いて、E(2e-e2),π/2)E(e,π/2)となります。
DERIVEで計算させてみますと(下記の注参照)、e=0~0.9まで、eを0.1ずつ変化させた場合の楕円の弧長(全周の1/4)は、
[1.570796326, 1.493290108, 1.418083394, 1.345592245, 1.276349943, 1.211056027,
1.150655629, 1.096477517, 1.050502226, 1.015993545]
[1.570796326, 1.566861942, 1.554968546, 1.534833464, 1.505941612, 1.467462209,
1.418083394, 1.355661135, 1.276349943, 1.171697052]となりました。
一方、近似式を用いた場合の弧長は、
[1.562417125, 1.485303319, 1.410431879, 1.338216042, 1.269194927, 1.204092525,
1.143917703, 1.090146741, 1.045089682, 1.012701947]となります。
なお、e=0のときは、4分円(1)の弧長と一致しています。
また、相対誤差は、%単位で次のとおりです。
[-0.5334365035, -0.5348451019, -0.5395673507, -0.5481752014, -0.5605841908,
-0.5749942071, -0.5855727665, -0.5773739909, -0.5152339391]
[-0.5334365036, -5.205220754, -9.295150527, -12.81034239, -15.72084090,
-17.94728902, -19.33353794, -19.58560197, -18.11887580, -13.56964282]
0.5%前後の相対誤差で一致しています。
ちなみに、DERIVEで計算させる場合は、ユーティリティとして「EllipticIntegrals.mth」を読み込んでおきます。このとき、E(k,φ)=ELLIPTIC_E(φ,
m)として計算します。DERIVEをお使いの場合、変数の順序が逆であるのとm=k2であることの2点にご注意ください。
目次に戻る
4分円の近似(2)の場合の計算結果を前節にならって書いてみましょう。楕円の大きさは、同一です。
このとき、4分円の近似(2)では、 x =t(2-t)、y=(1+t)(1-t) でしたが、これのy方向のみ(1-e)倍とします。
また、制御座標y2も同一の係数をかけましょう。
すると
x = t(2-t)
y = (1+t)(1-t)(1-e)
x2=1、y2=1-e
となります。離心率 eを0から0.9まで0.1ずつ変化させて、グラフを描いてみました。
また、近似式の場合の弧長を計算してみました。
比較のために上段に真の値を再掲してあります。
[1.570796326, 1.566861942, 1.554968546, 1.534833464, 1.505941612, 1.467462209,
1.418083394, 1.355661135, 1.276349943, 1.171697052]
[1.623225240, 1.542902958, 1.464448974, 1.388208260, 1.314631800, 1.244327152, 1.178145438, 1.117344551, 1.063937078, 1.021610712]
相対誤差は、%単位で次のとおりです。
[3.337728331, 3.322385230, 3.269594735, 3.167082387, 2.999322968, 2.747282062,
2.389056143, 1.903097298, 1.278898003]
[3.337728331, -1.529106257, -5.821312092, -9.553167000, -12.70366729,
-15.20550618, -16.91987629, -17.57936241, -16.64221212, -12.80931276]
こちらは、(1)の場合と相対誤差で比較するとほぼ同様の傾向です。最大相対誤差は、約20%といったところでしょう。
目次に戻る
なお、ベジェ曲線や同次座標、あるいは、複素数の拡張である四元数などについては、WEBで検索していただくと、もっと詳しいページがございます。
詳細をお知りになりたい方は、そのようなページをご参照いただければと思います。
今月は、ベジェ曲線を題材にDERIVEを使って、いろいろ、遊んでみましたが、皆様もぜひ、DERIVEを使ってみてください。
では、皆様に取りまして本年が素敵な年となりますように祈念しております。
今回もご覧いただき、ありがとうございました。
注)2007/4に上記記事中の「離心率」が「扁平率」の誤りであることに気づきました。また、同時に正確な楕円の弧長の計算値にもこれに起因する誤りがありましたので、訂正しました。
ちなみに離心率=√(1-(b/a)^2)、扁平率=1-(b/a)です。
目次に戻る